题目内容
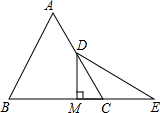 如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.(1)求∠E的度数.
(2)求证:M是BE的中点.
考点:等边三角形的性质,含30度角的直角三角形
专题:
分析:(1)由等边△ABC的性质可得:∠ACB=∠ABC=60°,然后根据等边对等角可得:∠E=∠CDE,最后根据外角的性质可求∠E的度数;
(2)连接BD,由等边三角形的三线合一的性质可得:∠DBC=
∠ABC=
×60°=30°,结合(1)的结论可得:∠DBC=∠E,然后根据等角对等边,可得:DB=DE,最后根据等腰三角形的三线合一的性质可得:M是BE的中点.
(2)连接BD,由等边三角形的三线合一的性质可得:∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)解:∵三角形ABC是等边△ABC,
∴∠ACB=∠ABC=60°,
又∵CE=CD,
∴∠E=∠CDE,
又∵∠ACB=∠E+∠CDE,
∴∠E=
∠ACB=30°;
(2)证明:连接BD,
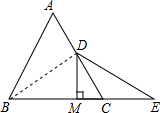
∵等边△ABC中,D是AC的中点,
∴∠DBC=
∠ABC=
×60°=30°
由(1)知∠E=30°
∴∠DBC=∠E=30°
∴DB=DE
又∵DM⊥BC
∴M是BE的中点.
∴∠ACB=∠ABC=60°,
又∵CE=CD,
∴∠E=∠CDE,
又∵∠ACB=∠E+∠CDE,
∴∠E=
| 1 |
| 2 |
(2)证明:连接BD,

∵等边△ABC中,D是AC的中点,
∴∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
由(1)知∠E=30°
∴∠DBC=∠E=30°
∴DB=DE
又∵DM⊥BC
∴M是BE的中点.
点评:此题考查了等边三角形的有关性质,重点考查了等边三角形的三线合一的性质.

练习册系列答案
相关题目
李明同学早上骑自行车上学,中途因道路施工步行一段路,到学校共用时15分粥.他骑自行车的平均速度是250米/分钟,步行的平均速度是80米/分钟》他家离学校的距离是2900米.如果他骑车和步行的时间分别为x,y分钟,列出的方程组是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
 如图,四边形ABCD的顶点都在⊙O上,点O在四边形内部,若四边形OABC为平行四边形,则∠D等于( )
如图,四边形ABCD的顶点都在⊙O上,点O在四边形内部,若四边形OABC为平行四边形,则∠D等于( )| A、30° | B、45° |
| C、60° | D、不能确定 |
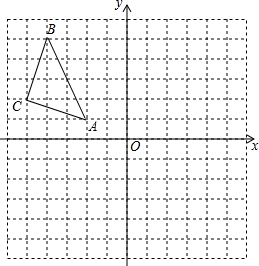 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2). 如图,AB是⊙O的直径,PA是⊙O的切线,过点B作BC∥OP交⊙O于点C,连结
如图,AB是⊙O的直径,PA是⊙O的切线,过点B作BC∥OP交⊙O于点C,连结 如图所示,图中平行四边形的一个角为60°,两条边的长分别为6cm和12cm,高为5cm.求图中阴影部分的面积.
如图所示,图中平行四边形的一个角为60°,两条边的长分别为6cm和12cm,高为5cm.求图中阴影部分的面积.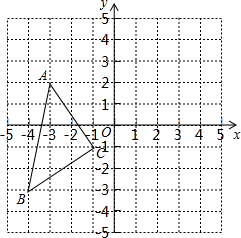 如图,单位长度为1的方格纸中,
如图,单位长度为1的方格纸中,