题目内容
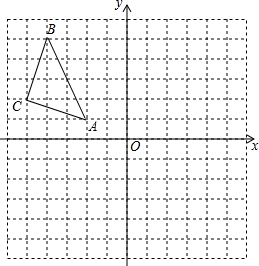 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1、B1、C1三点的坐标.
(2)若将点C向右平移h个单位,使其落在△A1B1C1内部,直接写出h的取值范围.
考点:作图-轴对称变换,坐标与图形变化-平移
专题:
分析:(1)直接根据轴对称的性质画出△A1B1C1,并写出各点坐标即可;
(2)利用待定系数法求出直线A1B1的解析式,求出E点坐标,进而可得出结论.
(2)利用待定系数法求出直线A1B1的解析式,求出E点坐标,进而可得出结论.
解答: 解:(1)如图所示.
解:(1)如图所示.
A1(2,1),B1(4,5),C1(5,2);
(2)设直线A1B1的解析式为y=kx+b(k≠0),
∵A1(2,1),B1(4,5),
∴
,解得
,
∴直线A1B1的解析式为y=2x-3,
∴当y=2时,x=
,
∴E(
,2).
∵C(-5,2),
∴CE=7.5,CC1=10,
∴7.5<h<10.
 解:(1)如图所示.
解:(1)如图所示.A1(2,1),B1(4,5),C1(5,2);
(2)设直线A1B1的解析式为y=kx+b(k≠0),
∵A1(2,1),B1(4,5),
∴
|
|
∴直线A1B1的解析式为y=2x-3,
∴当y=2时,x=
| 5 |
| 2 |
∴E(
| 5 |
| 2 |
∵C(-5,2),
∴CE=7.5,CC1=10,
∴7.5<h<10.
点评:本题考查的是作图-轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
下列方程中是一元一次方程的是( )
| A、x+2=y-3 | ||
| B、x+3=3-x | ||
C、
| ||
| D、x2-1=0 |
下列物体的运动不是旋转的是( )
| A、坐在摩天轮里的小朋友 |
| B、正在走动的时针 |
| C、骑自行车的人 |
| D、正在转动的风车叶片 |
下列各分式中,最简分式是( )
A、
| ||
B、
| ||
C、
| ||
D、
|

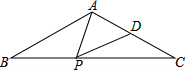 如图,已知△ABC中,AB=AC=2,∠B=30°,D为AC的中点,P是BC上的一动点,求PA+PD的最小值为( )
如图,已知△ABC中,AB=AC=2,∠B=30°,D为AC的中点,P是BC上的一动点,求PA+PD的最小值为( ) 用小立方块搭一个几何体,使它的从正面和从上面看到的这个几何体的形状图如图所示,从上面看到的形状图中的小正方形中的字母表示该位置小立方块的个数,试回答下列问题;
用小立方块搭一个几何体,使它的从正面和从上面看到的这个几何体的形状图如图所示,从上面看到的形状图中的小正方形中的字母表示该位置小立方块的个数,试回答下列问题;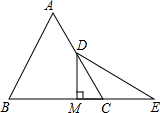 如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M. 已知a、b、c为有理数,且它们在数轴上的位置如图所示.
已知a、b、c为有理数,且它们在数轴上的位置如图所示.