题目内容
5.若不等式组$\left\{\begin{array}{l}{x-a>2}\\{b-2x>0}\end{array}\right.$的解集是-1<x<1,则(a+b)2013=-1.分析 解出不等式组的解集,与已知解集-1<x<1比较,可以求出a、b的值,然后相加求出2013次方,可得最终答案.
解答 解:解不等式x-a>2,得:x>a+2,
解不等式b-2x>0,得:x<$\frac{b}{2}$,
∵不等式的解集是-1<x<1,
∴a+2=-1,$\frac{b}{2}$=1,
解得:a=-3,b=2,
则(a+b)2013=(-3+2)2013=-1,
故答案为:-1.
点评 本题主要考查解一元一次不等式组,已知不等式组的解集,求不等式中另一未知数的问题.可以先将另一未知数当作已知处理,求出解集与已知解集比较,进而求得零一个未知数.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
13.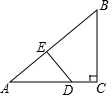 如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )
如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )
 如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )
如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )| A. | ∠A和∠B互为余角 | B. | ∠A和∠ADE互为余角 | ||
| C. | ∠B和∠EDC互为补角 | D. | ∠B和∠DEB互为补角 |
17.因为cos60°=$\frac{1}{2}$,cos240°=-$\frac{1}{2}$,所以cos240°=cos(180°+60°)=-cos60°;由此猜想、推理知:当α为锐角时有cos(180°+α)=-cosα,由此可知:cos210°=( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\sqrt{3}$ |
14.发现思考:已知等腰三角形ABC的两边分别是方程x2-7x+10=0的两个根,求等腰三角形ABC三条边的长各是多少?下边是涵涵同学的作业,老师说他的做法有错误,请你找出错误之处并说明错误原因.
涵涵的作业
探究应用:请解答以下问题:
已知等腰三角形ABC的两边是关于x的方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根.
(1)当m=2时,求△ABC的周长;
(2)当△ABC为等边三角形时,求m的值.
涵涵的作业
| 解:x2-7x+10=0 a=1 b=-7 c=10 ∵b2-4ac=9>0 ∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{7+3}{2}$ ∴x1=5,x2=2 所以,当腰为5,底为2时,等腰三角形的三条边为5,5,2. 当腰为2,底为5时,等腰三角形的三条边为2,2,5. |
已知等腰三角形ABC的两边是关于x的方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根.
(1)当m=2时,求△ABC的周长;
(2)当△ABC为等边三角形时,求m的值.
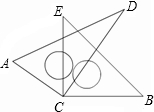 如图,将两块直角三角尺的直角顶点C叠放在一起.
如图,将两块直角三角尺的直角顶点C叠放在一起.