题目内容
20.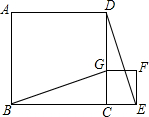 如图,点B、C、E是同一直线上的三点,四边形ABCD与四边形CEFG都是正方形,连接BG、DE.
如图,点B、C、E是同一直线上的三点,四边形ABCD与四边形CEFG都是正方形,连接BG、DE.(1)求证:BG=DE;
(2)已知小正方形CEFG的边长为1cm,连接CF,如果将正方形CEFG绕点C逆时针旋转,当A、E两点之间的距离最小时,求线段CF所扫过的面积.
分析 (1)根据正方形的性质和全等三角形的判定方法可证明△BCG≌△DCE,由全等三角形的性质即可得到BG=DE;
(2)根据C、E、A三点在同一直线上时,EA最短,再根据勾股定理解答即可.
解答 解:(1)∵四边形ABCD与四边形CEFG都是正方形,
∴BC=CD,CG=CE,∠BCG=∠DCE=90°,
在△BCG和△DCE中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCG=∠DCE}\\{CG=CE}\end{array}\right.$,
∴△BCG≌△DCE,
∴BG=DE;
(2)由题意可知,当C、E、A三点在同一直线上时,
即点E在对角线AC上时,EA最短,
此时CF旋转了135°,
由勾股定理可得:$CF=\sqrt{2}$
则CF扫过的面积为$S=\frac{135}{360}×π×{(\sqrt{2})^2}=\frac{3}{4}πc{m^2}$.
点评 本题考查了全等三角形的证明,考查了正方形各边相等且各内角为90°的性质,本题中求证△BCG≌△DCE是解题的关键.

练习册系列答案
相关题目
5.下列说法中,不正确的是( )
| A. | 同位角相等,两直线平行 | |
| B. | 两直线平行,内错角相等 | |
| C. | 两直线被第三条直线所截,内错角相等 | |
| D. | 同旁内角互补,两直线平行 |
12.我国雾霾天气多发,PM2.5颗粒物被称为大气的元凶,PM2.5是指直径小于或等于2.5微米的颗粒物,已知1毫米=1000微米,用科学记数法表示2.5微米是( )
| A. | 2.5×10-6m | B. | 25×10-6m | C. | 2.5×10-5m | D. | 25×10-5m |