题目内容
11.已知一次函数的图象经过点A(0,2)和点B(2,-2):(1)求出y关于x的函数表达式为y=-2x+2;
(2)当-2<y<4时,x的取值范围是-1<x<2.
分析 (1)设一次函数解析式为y=kx+b,把A与B坐标代入求出k与b的值,即可确定出一次函数表达式;
(2)根据一次函数图象的性质进行答题即可.
解答 解:(1)设一次函数解析式为y=kx+b,
把A(0,2)、B(2,-2)代入得:
$\left\{\begin{array}{l}{b=2}\\{2k+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$.
则一次函数解析式为y=-2x+2;
(2)∵y=-2x+2,
∴函数y随x的增大而减小.
∵当y=-2时,x=2;
当y=4时,x=-1,
∴当-2<y<4时,-1<x<2.
故答案为(1)y=-2x+2;(2)-1<x<2.
点评 此题考查了待定系数法求一次函数解析式,一次函数的图象与性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
2.某县10名学生参加汉字听写大赛,他们得分情况如下表:
那么这10名学生所得分数的中位数和众数分别是( )
| 人数 | 3 | 4 | 2 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
| A. | 85和82.5 | B. | 85.5和85 | C. | 85和85 | D. | 85.5和80 |
6.下列各项结论中错误的是( )
| A. | 二元一次方程x+2y=2的解可以表示为$\left\{\begin{array}{l}{x=m}\\{y=1-\frac{m}{2}}\end{array}\right.$ (m是实数) | |
| B. | 若$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{3x+2y=m}\\{nx-y=1}\end{array}\right.$的解,则m+n的值为0 | |
| C. | 设一元二次方程x2+3x-4=0的两根分别为m、n,则m+n的值为-3 | |
| D. | 若-5x2ym与xny是同类项,则m+n的值为3 |
3.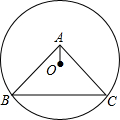 如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
 如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )| A. | 6 | B. | 13 | C. | $\sqrt{13}$ | D. | 2$\sqrt{13}$ |
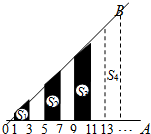 如图,∠AOB=45°,过0A上到点O的距离分别为1,3,5,7,9,11,L的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4,L.观察图中的规律,求出第11个黑色梯形的面积S11=84.
如图,∠AOB=45°,过0A上到点O的距离分别为1,3,5,7,9,11,L的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4,L.观察图中的规律,求出第11个黑色梯形的面积S11=84.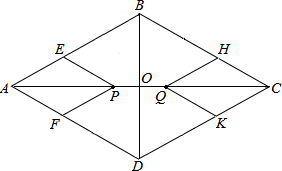 菱形ABCD的边长为2,∠BAD=60°,对角线AC,BD相交于点O,动点P在线段AC上从点A向点C运动,过P作PE∥AD,交AB于点E,过P作PF∥AB,交AD于点F,四边形QHCK与四边形PEAF关于直线BD对称.设菱形ABCD被这两个四边形盖住部分的面积为S1,AP=x:
菱形ABCD的边长为2,∠BAD=60°,对角线AC,BD相交于点O,动点P在线段AC上从点A向点C运动,过P作PE∥AD,交AB于点E,过P作PF∥AB,交AD于点F,四边形QHCK与四边形PEAF关于直线BD对称.设菱形ABCD被这两个四边形盖住部分的面积为S1,AP=x: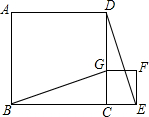 如图,点B、C、E是同一直线上的三点,四边形ABCD与四边形CEFG都是正方形,连接BG、DE.
如图,点B、C、E是同一直线上的三点,四边形ABCD与四边形CEFG都是正方形,连接BG、DE.