题目内容
15.解答下列各题:①一次函数图象过点(-1,4)且与直线y=2-3x平行,此一次函数解析式是y=-3x+1.
②在平面直角坐标系中,直线y=kx+3经过点(-1,1),不等式kx+3≤0的解集是x≤-$\frac{3}{2}$.
分析 ①设所求一次函数解析式为y=kx+b,利用两直线平行的问题得到k=-3,然后把(-1,4)代入y=-3x+b中求出b即可;
②先把(-1,1)代入y=kx+3求出k,得到不等式2x+3≤0,然后解不等式即可.
解答 解:①设所求一次函数解析式为y=kx+b,
∵直线y=kx+b与直线y=2-3x平行,
∴k=-3,
把(-1,4)代入y=-3x+b得3+b=4,解得b=1,
∴所求一次函数解析式为y=-3x+1;
②把(-1,1)代入y=kx+3得-k+3=1,解得k=2,
解不等式2x+3≤0得x≤-$\frac{3}{2}$.
故答案为y=-3x+1,x≤-$\frac{3}{2}$.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.也考查了解一元一次不等式.

练习册系列答案
相关题目
6.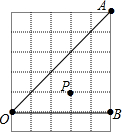 如图由边长为1cm正方形组成的6×5的方格阵,点O、A、B、P都在格点上〔即行和列的交点处),M、N分别是0A、OB上的动点,则△PMN周长的最小值是( )
如图由边长为1cm正方形组成的6×5的方格阵,点O、A、B、P都在格点上〔即行和列的交点处),M、N分别是0A、OB上的动点,则△PMN周长的最小值是( )
 如图由边长为1cm正方形组成的6×5的方格阵,点O、A、B、P都在格点上〔即行和列的交点处),M、N分别是0A、OB上的动点,则△PMN周长的最小值是( )
如图由边长为1cm正方形组成的6×5的方格阵,点O、A、B、P都在格点上〔即行和列的交点处),M、N分别是0A、OB上的动点,则△PMN周长的最小值是( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 1+$\sqrt{2}$+$\sqrt{5}$ | D. | 2$+2\sqrt{2}$ |
10.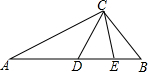 如图,在△ABC中,∠ACB=110°,AC=AE,BC=BD,则∠DCE的度数为( )
如图,在△ABC中,∠ACB=110°,AC=AE,BC=BD,则∠DCE的度数为( )
 如图,在△ABC中,∠ACB=110°,AC=AE,BC=BD,则∠DCE的度数为( )
如图,在△ABC中,∠ACB=110°,AC=AE,BC=BD,则∠DCE的度数为( )| A. | 30° | B. | 35° | C. | 50° | D. | 70° |
20.分式$\frac{1}{{a}^{2}-2a+1}$,$\frac{1}{a-1}$,$\frac{1}{{a}^{2}+2a+1}$的最简公分母是( )
| A. | (a2-1)2 | B. | (a2-1)(a2+1) | C. | a2+1 | D. | (a-1)4 |
5.用反证法证明命题:若整数系数一元二次方程ax2+bx+c=0(a≠0)有有理根,那么a、b、c中至少有一个是偶数时,下列假设中正确的是( )
| A. | 假设a、b、c都是偶数 | B. | 假设a、b、c至多有一个是偶数 | ||
| C. | 假设a、b、c都不是偶数 | D. | 假设a、b、c至多有两个是偶数 |
 某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动
某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动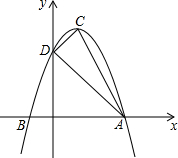 如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.
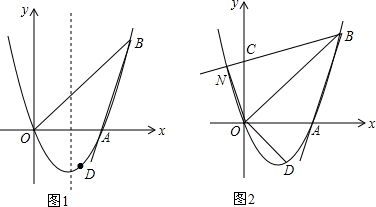
如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.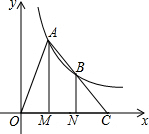 如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A,B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,且△BNC的面积为4,则k值为16.
如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A,B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,且△BNC的面积为4,则k值为16.