题目内容

5．用反证法证明命题：若整数系数一元二次方程ax2+bx+c=0（a≠0）有有理根，那么a、b、c中至少有一个是偶数时，下列假设中正确的是（　　）
A．假设a、b、c都是偶数B．假设a、b、c至多有一个是偶数
C．假设a、b、c都不是偶数D．假设a、b、c至多有两个是偶数

分析 利用反证法证明的步骤，从问题的结论的反面出发否定即可．

解答 解：∵用反证法证明：若整数系数一元二次方程ax2+bx+c=0（a≠0）有有理根，那么a、b、c中至少有一个是偶数，
∴假设a、b、c都不是偶数．
故选：C．

点评 此题主要考查了反证法，反证法的一般步骤是：①假设命题的结论不成立；②从这个假设出发，经过推理论证，得出矛盾；③由矛盾判定假设不正确，从而肯定原命题的结论正确．

练习册系列答案
相关题目
15．解答下列各题：
①一次函数图象过点（-1，4）且与直线y=2-3x平行，此一次函数解析式是y=-3x+1．
②在平面直角坐标系中，直线y=kx+3经过点（-1，1），不等式kx+3≤0的解集是x≤-$\frac{3}{2}$．
16．【发现】
如图∠ACB=∠ADB=90°，那么点D在经过A，B，C三点的圆上（如图①）

【思考】
如图②，如果∠ACB=∠ADB=a（a≠90°）（点C，D在AB的同侧），那么点D还在经过A，B，C三点的圆上吗？
请证明点D也不在⊙O内．
【应用】
利用【发现】和【思考】中的结论解决问题：
若四边形ABCD中，AD∥BC，∠CAD=90°，点E在边AB上，CE⊥DE．
（1）作∠ADF=∠AED，交CA的延长线于点F（如图④），求证：DF为Rt△ACD的外接圆的切线；
（2）如图⑤，点G在BC的延长线上，∠BGE=∠BAC，已知sin∠AED=$\frac{2}{5}$，AD=1，求DG的长．
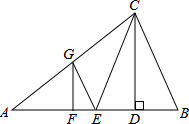13．如图，在△ABC中，CD是高，CE是中线，CE=CB，AF=DF，过点F作FG∥CD，交AC边于点G，连接GE．若AC=18，BC=12，则△CEG的周长为27．
20．请写出二元一次方程5x-3y=2的一个整数解，这个解可以是：$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$等．
10．在下列运算中，正确的是（　　）
A．a6÷a6=0B．（ab4）4=a4b16C．3-1=-3D．$\sqrt{（-3）^{2}}$=±3
17．把多项式4x3-9xy2分解因式的结果是x（2x-3y）（2x+3y）．
14．计算：（-1）2015+|1-tan60°|-$\sqrt{12}$+（$\sqrt{3}$）0．
15．小明将100元按一年定期存入银行，一年定期到期后，银行自动将应得本息再按一年定期续存，若银行一年定期利率为x，则第二年定期到期时，小明可得本息共100（1+x）2元．（不计利息税）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网