题目内容
20.分式$\frac{1}{{a}^{2}-2a+1}$,$\frac{1}{a-1}$,$\frac{1}{{a}^{2}+2a+1}$的最简公分母是( )| A. | (a2-1)2 | B. | (a2-1)(a2+1) | C. | a2+1 | D. | (a-1)4 |
分析 利用最简公分母就是各系数的最小公倍数,相同字母或整式的最高次幂,所有不同字母或整式都写在积里求解即可.
解答 解:$\frac{1}{{a}^{2}-2a+1}$=$\frac{1}{(a-1)^{2}}$,$\frac{1}{a-1}$,$\frac{1}{{a}^{2}+2a+1}$=$\frac{1}{(a+1)^{2}}$,
所以分式$\frac{1}{{a}^{2}-2a+1}$,$\frac{1}{a-1}$,$\frac{1}{{a}^{2}+2a+1}$的最简公分母是(a-1)2(a+1)2.即(a2-1)2
故选:A.
点评 本题主要考查了最简公分母,解题的关键是熟记最简公分母的定义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.一次函数y=kx+b图象过点(x1,y1)和(x2,y2),且k<0,b<0,当x1<0<x2时,有( )
| A. | y1>y2>b | B. | y2>b>y1 | C. | y2>0>y1 | D. | y1>b>y2 |
10.在下列运算中,正确的是( )
| A. | a6÷a6=0 | B. | (ab4)4=a4b16 | C. | 3-1=-3 | D. | $\sqrt{(-3)^{2}}$=±3 |
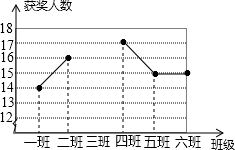 某中学组织网络安全知识竞赛活动,其中七年级6个班每班参赛人数相同,学校对该年级的获奖人数进行统计,得到平均每班获奖15人,并制作成如图所示不完整的折线统计图.
某中学组织网络安全知识竞赛活动,其中七年级6个班每班参赛人数相同,学校对该年级的获奖人数进行统计,得到平均每班获奖15人,并制作成如图所示不完整的折线统计图. 作图:如图,边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°.画出旋转后的△AB′C′.
作图:如图,边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°.画出旋转后的△AB′C′.