题目内容
6.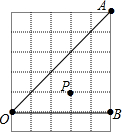 如图由边长为1cm正方形组成的6×5的方格阵,点O、A、B、P都在格点上〔即行和列的交点处),M、N分别是0A、OB上的动点,则△PMN周长的最小值是( )
如图由边长为1cm正方形组成的6×5的方格阵,点O、A、B、P都在格点上〔即行和列的交点处),M、N分别是0A、OB上的动点,则△PMN周长的最小值是( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 1+$\sqrt{2}$+$\sqrt{5}$ | D. | 2$+2\sqrt{2}$ |
分析 分别作点P关于OA、OB的对称点P1、P2,连P1P2,交OA于M,交OB于N,△PMN的周长=P1P2,
解答 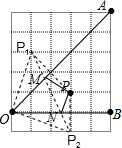 解:分别作点P关于OA、OB的对称点P1、P2,连P1P2,交OA于M,交OB于N,
解:分别作点P关于OA、OB的对称点P1、P2,连P1P2,交OA于M,交OB于N,
则OP1=OP=OP2,∠P1OA=∠POA,∠POB=∠P2OB,
MP=P1M,PN=P2N,则△PMN的周长的最小值=P1P2,
由图知,△P1P2O是等腰直角三角形,且OP1=$\sqrt{{1}^{2}{+3}^{2}}$=$\sqrt{10}$,
∴P1P2=$\sqrt{2}$OP1=2$\sqrt{5}$,
∴△PMN周长的最小值是2$\sqrt{5}$.
故选B.
点评 此题考查了轴对称的性质,以及三角形的周长的计算,等腰直角三角形的性质,勾股定理,熟练轴对称的性质是解本题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
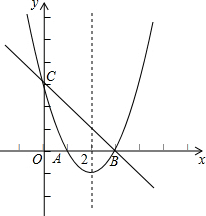 已知抛物线y=ax2+bx+3,与x轴交于A、B两点(如图),OB=OC=3OA,
已知抛物线y=ax2+bx+3,与x轴交于A、B两点(如图),OB=OC=3OA, 已知:如图,已知直线AB的函数解析式为y=2x+10,与y轴交于点A,与x轴交于点B.
已知:如图,已知直线AB的函数解析式为y=2x+10,与y轴交于点A,与x轴交于点B.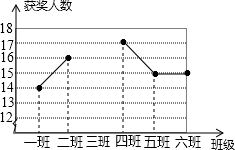 某中学组织网络安全知识竞赛活动,其中七年级6个班每班参赛人数相同,学校对该年级的获奖人数进行统计,得到平均每班获奖15人,并制作成如图所示不完整的折线统计图.
某中学组织网络安全知识竞赛活动,其中七年级6个班每班参赛人数相同,学校对该年级的获奖人数进行统计,得到平均每班获奖15人,并制作成如图所示不完整的折线统计图.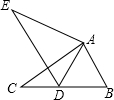 请从以下两个小题中任选一个作答,若多选,则按所选做的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选做的第一题计分.