题目内容
15.已知a是方程x2-3x-1=0的一个根,则a2+$\frac{1}{{a}^{2}}$=11,a3-10a+5=8.分析 由把x=a代入已知方程后易得到a2-$\frac{1}{a}$-3=0,然后利用完全平方公式的变形公式来求a2+$\frac{1}{{a}^{2}}$的值;
由已知的等式变形得到a2-1=3a,a2-3a=1,把所求的式子中的-10a变形为-9a-a=-3×3a-a,将3a=a2-1代入后,去括号整理后再将a2-3a=1代入,合并后即可得到结果.
解答 解:把x=a代入x2-3x-1=0得到:a2-3a-1=0,
所以a-$\frac{1}{a}$-3=0,
所以a-$\frac{1}{a}$=3,
所以a2+$\frac{1}{{a}^{2}}$=(a-$\frac{1}{a}$)2+2=32+2=11.
由a2-3a-1=0得到,a2-3a=1,
则a3-10a+5
=a3-9a-a+5
=a3-3(a2-1)-a+5
=a3-3a2+3-a+5
=a(a2-3a)+3-a+5
=a+3-a+5
=8.
故答案是:11;8.
点评 本题考查了一元二次方程的解的定义.利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
相关题目
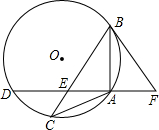 已知:如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
已知:如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.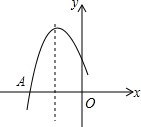 二次函数y=ax2+bx+c图象的一部分如图所示,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2<4ac;②2a+b=0;③a+b+c=0;④若点B(-$\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)为函数图象上得两点,则y1=y2;其中正确结论是( )
二次函数y=ax2+bx+c图象的一部分如图所示,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2<4ac;②2a+b=0;③a+b+c=0;④若点B(-$\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)为函数图象上得两点,则y1=y2;其中正确结论是( )
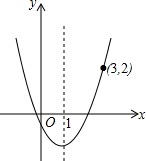 已知函数y=ax2+bx-1的图象经过点(3,2),对称轴为直线x=1.
已知函数y=ax2+bx-1的图象经过点(3,2),对称轴为直线x=1. 如图,在Rt△ABC中,∠A=90°,∠C=60°,直线DE∥BC,分别交边AB,AC于点D,E,求∠1的度数.
如图,在Rt△ABC中,∠A=90°,∠C=60°,直线DE∥BC,分别交边AB,AC于点D,E,求∠1的度数.