题目内容
 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,点G为对角线交点,顶点A在x轴上,顶点C的坐标为(0,6),∠COB=30°,以OC上一点P为圆心,以
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,点G为对角线交点,顶点A在x轴上,顶点C的坐标为(0,6),∠COB=30°,以OC上一点P为圆心,以| 3 |
| 2 |
(1)求点P的坐标;
(2)判断AC和⊙P的位置关系,并说明理由;
(3)已知点E为⊙P与PC的交点,求DE的长.
考点:圆的综合题,含30度角的直角三角形,勾股定理,矩形的性质,切线的判定与性质,特殊角的三角函数值
专题:综合题
分析:(1)连接PD,在Rt△PDO中,知道一边、一锐角可以求出OP长,从而求出点P的坐标.
(2)过点P作PH⊥AC,垂足为H,只需求出PH长,然后比较PH与半径PD大小关系,就可得到AC和⊙P的位置关系.
(3)过点D作DF⊥OC,垂足为F,只需求出DF、EF的长,就可以求出DE的长.
(2)过点P作PH⊥AC,垂足为H,只需求出PH长,然后比较PH与半径PD大小关系,就可得到AC和⊙P的位置关系.
(3)过点D作DF⊥OC,垂足为F,只需求出DF、EF的长,就可以求出DE的长.
解答:解:(1)连接PD,如图1所示.
∵⊙P与与OB相切于点D,
∴PD⊥OB,即∠ODP=90°.
∵∠COB=30°,PD=
,
∴OP=2PD=3.
∴点P的坐标为(0,3).
(2)AC和⊙P相切.
理由如下:
过点P作PH⊥AC,垂足为H,如图2所示.
∵点C的坐标为(0,6),
∴OC=6.
∴PC=OC-OP=3.
∵四边形ABCD是矩形,
∴GC=GO.
∴∠GCO=∠GOC=30°.
∴PH=
PC=
,
∴PH=PD.
∴⊙P与AC相切.
(3)过点D作DF⊥OC,垂足为F,如图3所示.
在Rt△PFD中,
∵PD=
,∠FPD=90°-30°=60°,
∴sin∠FPD=
=
=
.
∴DF=
.
同理:PF=
.
在Rt△DFE中,
DF=
,EF=PE+PF=
+
=
,
∴DE=
=
=
.
∴DE的长为
.

∵⊙P与与OB相切于点D,
∴PD⊥OB,即∠ODP=90°.
∵∠COB=30°,PD=
| 3 |
| 2 |
∴OP=2PD=3.
∴点P的坐标为(0,3).
(2)AC和⊙P相切.
理由如下:
过点P作PH⊥AC,垂足为H,如图2所示.
∵点C的坐标为(0,6),

∴OC=6.
∴PC=OC-OP=3.
∵四边形ABCD是矩形,
∴GC=GO.
∴∠GCO=∠GOC=30°.
∴PH=
| 1 |
| 2 |
| 3 |
| 2 |
∴PH=PD.
∴⊙P与AC相切.
(3)过点D作DF⊥OC,垂足为F,如图3所示.

在Rt△PFD中,
∵PD=
| 3 |
| 2 |
∴sin∠FPD=
| DF |
| DP |
| DF | ||
|
| ||
| 2 |
∴DF=
3
| ||
| 4 |
同理:PF=
| 3 |
| 4 |
在Rt△DFE中,
DF=
3
| ||
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 4 |
∴DE=
| DF2+EF2 |
=
(
|
=
3
| ||
| 2 |
∴DE的长为
3
| ||
| 2 |
点评:本题考查了切线的判定与性质、矩形的性质、特殊角的三角函数值、30°所对的直角边等于斜边的一半、勾股定理等知识,具有一定的综合性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
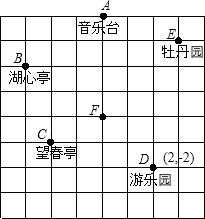 小英和爸爸、妈妈到人民公园游玩,回家后她利用平面直角坐标系画出了公园的景区地图,如图.可是她忘记了在图中标出原点和x轴、y轴.只知道游乐园D和望春亭C的坐标分别为(2,-2)和(-2,-1),你能帮她求出其他各景点的坐标吗?
小英和爸爸、妈妈到人民公园游玩,回家后她利用平面直角坐标系画出了公园的景区地图,如图.可是她忘记了在图中标出原点和x轴、y轴.只知道游乐园D和望春亭C的坐标分别为(2,-2)和(-2,-1),你能帮她求出其他各景点的坐标吗?
 如图,在△ABC中,∠B>∠C,AD⊥BC,垂足为D,AE平分∠BAC.
如图,在△ABC中,∠B>∠C,AD⊥BC,垂足为D,AE平分∠BAC. 儿童节,端午节期间,甲,乙两商场出售同种小香囊的方案如图,要使乙商场销售小香囊的营业额不低于甲商场,则乙商场至少应销售
儿童节,端午节期间,甲,乙两商场出售同种小香囊的方案如图,要使乙商场销售小香囊的营业额不低于甲商场,则乙商场至少应销售