题目内容
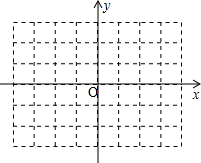 (1)在给出的直角坐标系中,画出两条一次函数图象,使得它们都满足;当自变量-1≤x≤1时,其函数值的取值范围为-2≤y≤3;
(1)在给出的直角坐标系中,画出两条一次函数图象,使得它们都满足;当自变量-1≤x≤1时,其函数值的取值范围为-2≤y≤3;(2)探究动点(m,m+1)在什么样一次函数图象上,并求出其解析式;
(3)在符合问题(1)的函数图象上,找到一点(m,m+1),使m值最大,并求出此时m值.
考点:一次函数的性质,一次函数的图象,一次函数图象上点的坐标特征,待定系数法求一次函数解析式
专题:
分析:(1)取A(1,3),B(-1,-2),C(-1,3),D(1,-2),画出直线AB与CD即可;
(2)分别令m=0,m=1得出两点,用待定系数法求出过两点的直线解析式即可;
(3)在坐标系内画出直线y=x+1的图象,与直线AB、CD分别交于点F、E,由图象可知,点F对应的m值最大,再用待定系数法求值直线AB的解析式,求出F点的坐标即可.
(2)分别令m=0,m=1得出两点,用待定系数法求出过两点的直线解析式即可;
(3)在坐标系内画出直线y=x+1的图象,与直线AB、CD分别交于点F、E,由图象可知,点F对应的m值最大,再用待定系数法求值直线AB的解析式,求出F点的坐标即可.
解答: 解:(1)取A(1,3),B(-1,-2),C(-1,3),D(1,-2),直线AB和直线CD就是要找的两条一次函数的图象;
解:(1)取A(1,3),B(-1,-2),C(-1,3),D(1,-2),直线AB和直线CD就是要找的两条一次函数的图象;
(2)分别令m=0,-1,则点(0,1),(-1,0),
设过两点的直线方程为y=kx+b(k≠0),
则
,解得
,
故直线解析式为y=x+1,
∵x=m时,y=m+1,
∴此直线的解析式即为所求;
(3)由图象可知,点F对应的m值最大.
设直线AB的直线方程为y=ax+c(a≠0),
∵A(1,3),B(-1,-2),
∴
,解得
,
∴直线AB的解析式为y=2.5x+0.5,
∴
,解得
,即F(
,
),
∴m的最大值为
.
 解:(1)取A(1,3),B(-1,-2),C(-1,3),D(1,-2),直线AB和直线CD就是要找的两条一次函数的图象;
解:(1)取A(1,3),B(-1,-2),C(-1,3),D(1,-2),直线AB和直线CD就是要找的两条一次函数的图象;(2)分别令m=0,-1,则点(0,1),(-1,0),
设过两点的直线方程为y=kx+b(k≠0),
则
|
|
故直线解析式为y=x+1,
∵x=m时,y=m+1,
∴此直线的解析式即为所求;
(3)由图象可知,点F对应的m值最大.
设直线AB的直线方程为y=ax+c(a≠0),
∵A(1,3),B(-1,-2),
∴
|
|
∴直线AB的解析式为y=2.5x+0.5,
∴
|
|
| 1 |
| 3 |
| 4 |
| 3 |
∴m的最大值为
| 1 |
| 3 |
点评:本题考查的是一次函数的性质,熟知一次函数的增减性是解答此题的关键.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
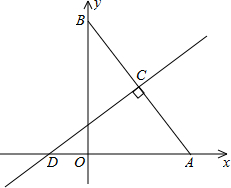 如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴、y轴的正半轴上(OA<OB),且OA、OB的长分别是一元二次方程x2-14x+48=0的两个根.线段AB的垂直平分线CD交AB于点C,交x轴于点D,点P是直线CD上一个动点,点Q是直线AB上一个动点.
如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴、y轴的正半轴上(OA<OB),且OA、OB的长分别是一元二次方程x2-14x+48=0的两个根.线段AB的垂直平分线CD交AB于点C,交x轴于点D,点P是直线CD上一个动点,点Q是直线AB上一个动点. 如图,平行四边形ABCD的一条角平分线AE分对边BC为3和4两部分,求这个平行四边形ABCD的周长.
如图,平行四边形ABCD的一条角平分线AE分对边BC为3和4两部分,求这个平行四边形ABCD的周长.