题目内容
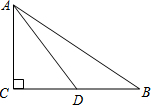如图，在Rt△ABC中，∠C=90°，点D是BC边上的一点，CD=6，cos∠ADC=| 3 |
| 5 |
| 2 |
| 3 |
（1）求AC和AB的长；
（2）求sin∠BAD的值．
考点：解直角三角形
专题：
分析：（1）通过解Rt△ACD得到AD边的长度；然后在该直角三角形中利用勾股定理来求AC的长度；然后通过解Rt△ABC可以求得BC的长度，再利用勾股定理求线段AB的长度．
（2）如图，过点D作DE⊥AB于点E，构建Rt△ADE，通过解该直角三角形来求sin∠BAD的值．
（2）如图，过点D作DE⊥AB于点E，构建Rt△ADE，通过解该直角三角形来求sin∠BAD的值．
解答：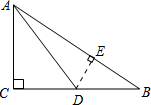
解：（1）如图，在Rt△ACD中，∵∠ACD=90°，CD=6，cos∠ADC=
，
∴
=
，即
=
，
则AD=10，
∴由勾股定理知，AC=
=
=8．
又∵tanB=
，
∴
=
，即
=
，
则BC=12．
∴在Rt△ABC中，利用勾股定理知，AB=
=
=4
．
综上所述，AC=8，AB=4
；
（2）如图，过点D作DE⊥AB于点E．
由（1）易知，BD=6．
∵tanB=
，
∴
=
．则BE=
DE．
则由勾股定理得到：62=DE2+
DE2，
解得 DE=
，
∴sin∠BAD=
=
=
．
解：（1）如图，在Rt△ACD中，∵∠ACD=90°，CD=6，cos∠ADC=| 3 |
| 5 |
∴
| CD |
| AD |
| 3 |
| 5 |
| 6 |
| AD |
| 3 |
| 5 |
则AD=10，
∴由勾股定理知，AC=
| AD2-CD2 |
| 102-62 |
又∵tanB=
| 2 |
| 3 |
∴
| AC |
| BC |
| 2 |
| 3 |
| 8 |
| BC |
| 2 |
| 3 |
则BC=12．
∴在Rt△ABC中，利用勾股定理知，AB=
| AC2+BC2 |
| 82+122 |
| 13 |
综上所述，AC=8，AB=4
| 13 |
（2）如图，过点D作DE⊥AB于点E．
由（1）易知，BD=6．
∵tanB=
| 2 |
| 3 |
∴
| DE |
| BE |
| 2 |
| 3 |
| 3 |
| 2 |
则由勾股定理得到：62=DE2+
| 9 |
| 4 |
解得 DE=
12
| ||
| 13 |
∴sin∠BAD=
| DE |
| AD |
| ||||
| 10 |
6
| ||
| 65 |
点评：本题考查了解直角三角形．要熟练掌握好边角之间的关系．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
为了改善居民住房条件，某市计划用未来两年的时间，将城镇居民的住房面积由现在的人均约为10m2提高到12.1m2．若每年的年增长率相同，则年增长率为（ ）
| A、9% | B、10% |
| C、11% | D、12% |
如图，已知直线l1∥l2，则∠a的度数为（ ）| A、115° | B、135° |
| C、145° | D、150° |
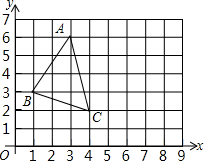如图，△ABC的顶点坐标分别为A（3，6），B（1，3），C（4，2），将△ABC绕点C顺时针旋转90°，得到△A′B′C．
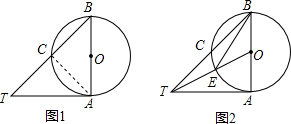已知AB是⊙O的直径，AT与⊙O相切于点A，⊙O交BT于C，CT=CB．