题目内容
已知二次函数y=x2+bx+c的图象与x轴只有一个公共点A.
(1)若这个公共点为(2,0),求二次函数的表达式;
(2)若二次函数的图象与y轴的交点为B,坐标原点为O,且△OAB是等腰三角形,求该二次函数的表达式,并说明它是如何由(1)中的二次函数的图象平移得到的.
(1)若这个公共点为(2,0),求二次函数的表达式;
(2)若二次函数的图象与y轴的交点为B,坐标原点为O,且△OAB是等腰三角形,求该二次函数的表达式,并说明它是如何由(1)中的二次函数的图象平移得到的.
考点:抛物线与x轴的交点,二次函数图象与几何变换
专题:计算题
分析:(1)根据抛物线与x轴的交点问题得到点A为抛物线的顶点,然后利用顶点式可写出抛物线解析式;
(2)先根据顶点坐标公式写出顶点A的坐标(-
,0),根据△=b2-4ac决定抛物线与x轴的交点个数得到b2-4c=0,再确定B(0,c),接着利用OA=OB得到c=|-
|,然后解出c=1,b=2或b=-2,所以当b=2,c=1时,抛物线解析式为y=(x+1)2;当b=-2,c=1时,抛物线解析式为y=(x-1)2,再根据抛物线平移的规律通过平移抛物线y=(x-2)2得到抛物线y=(x+1)2或抛物线y=(x-1)2.
(2)先根据顶点坐标公式写出顶点A的坐标(-
| b |
| 2 |
| b |
| 2 |
解答:解:(1)∵二次函数y=x2+bx+c的图象与x轴只有一个公共点A,
∴点A为抛物线的顶点,
∴抛物线解析式为y=(x-2)2;
(2)∵二次函数y=x2+bx+c的图象与x轴只有一个公共点A,
∴点A为抛物线的顶点,且A(-
,0),b2-4c=0,
当x=0时,y=x2+bx+c=c,则B(0,c),
∵△OAB是等腰三角形,
∴OA=OB,即c=|-
|,
∴b2=4c2,
∴4c2-c2=0,即得c1=0(舍去),c2=1,
∴|-
|=1,解得b=2或b=-2,
当b=2,c=1时,抛物线解析式为y=x2+2x+1=(x+1)2,它可由抛物线y=(x-2)2向左平移3个单位得到;
当b=-2,c=1时,抛物线解析式为y=x2-2x+1=(x-1)2,它可由抛物线y=(x-2)2向左平移1个单位得到.
∴点A为抛物线的顶点,
∴抛物线解析式为y=(x-2)2;
(2)∵二次函数y=x2+bx+c的图象与x轴只有一个公共点A,
∴点A为抛物线的顶点,且A(-
| b |
| 2 |
当x=0时,y=x2+bx+c=c,则B(0,c),
∵△OAB是等腰三角形,
∴OA=OB,即c=|-
| b |
| 2 |
∴b2=4c2,
∴4c2-c2=0,即得c1=0(舍去),c2=1,
∴|-
| b |
| 2 |
当b=2,c=1时,抛物线解析式为y=x2+2x+1=(x+1)2,它可由抛物线y=(x-2)2向左平移3个单位得到;
当b=-2,c=1时,抛物线解析式为y=x2-2x+1=(x-1)2,它可由抛物线y=(x-2)2向左平移1个单位得到.
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了二次函数图象与几何变换.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
为了改善居民住房条件,某市计划用未来两年的时间,将城镇居民的住房面积由现在的人均约为10m2提高到12.1m2.若每年的年增长率相同,则年增长率为( )
| A、9% | B、10% |
| C、11% | D、12% |
 如图,已知直线l1∥l2,则∠a的度数为( )
如图,已知直线l1∥l2,则∠a的度数为( )| A、115° | B、135° |
| C、145° | D、150° |
 如图,是一个正方体的展开图,正方体的每个面都有一个数字,只有一对相对两面的数字的积是有理数,这个有理数是( )
如图,是一个正方体的展开图,正方体的每个面都有一个数字,只有一对相对两面的数字的积是有理数,这个有理数是( )| A、4 | B、6 | C、9 | D、10 |
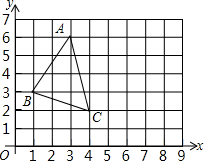 如图,△ABC的顶点坐标分别为A(3,6),B(1,3),C(4,2),将△ABC绕点C顺时针旋转90°,得到△A′B′C.
如图,△ABC的顶点坐标分别为A(3,6),B(1,3),C(4,2),将△ABC绕点C顺时针旋转90°,得到△A′B′C.
 已知三角形ABC,求作三角形ABC绕点C逆时针旋转90°的三角形.(保留作图痕迹,不写作法)
已知三角形ABC,求作三角形ABC绕点C逆时针旋转90°的三角形.(保留作图痕迹,不写作法)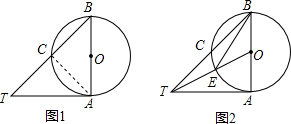 已知AB是⊙O的直径,AT与⊙O相切于点A,⊙O交BT于C,CT=CB.
已知AB是⊙O的直径,AT与⊙O相切于点A,⊙O交BT于C,CT=CB.