题目内容
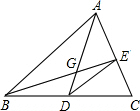如图，已知AD是△ABC的中线，G是△ABC的重心，联结BG并延长交AC于点E，联结DE，则S△ABC：S△CED的值为考点：三角形的重心
专题：
分析：由AD是△ABC的中线，G是△ABC的重心，联结BG并延长交AC于点E，根据三角形重心的定义与性质可得E为AC的中点，AG=2DG，BG=2GE．设S△EGD=x，根据
三角形的面积公式，等高的两个三角形面积之比等于底之比得出S△EGA=2S△EGD=2x，那么S△EAD=S△EGD+S△EGA=3x，又E为AC中点，等底等高的两个三角形面积相等，于是S△ECD=S△EAD=3x，S△ADC=S△ECD+S△EAD=6x，同理由AD是△ABC的中线，得出S△ABC=2S△ADC=12x，那么S△ABC：S△CED=12x：3x=4．
三角形的面积公式，等高的两个三角形面积之比等于底之比得出S△EGA=2S△EGD=2x，那么S△EAD=S△EGD+S△EGA=3x，又E为AC中点，等底等高的两个三角形面积相等，于是S△ECD=S△EAD=3x，S△ADC=S△ECD+S△EAD=6x，同理由AD是△ABC的中线，得出S△ABC=2S△ADC=12x，那么S△ABC：S△CED=12x：3x=4．
解答：解：∵AD是△ABC的中线，G是△ABC的重心，联结BG并延长交AC于点E，
∴E为AC的中点，AG=2DG，BG=2GE．
设S△EGD=x，
∵AG=2DG，
∴S△EGA=2S△EGD=2x，
∴S△EAD=S△EGD+S△EGA=3x，
∵E为AC中点，
∴S△ECD=S△EAD=3x，
∴S△ADC=S△ECD+S△EAD=6x，
∵AD是△ABC的中线，
∴S△ABC=2S△ADC=12x，
∴S△ABC：S△CED=12x：3x=4．
故答案为4．
∴E为AC的中点，AG=2DG，BG=2GE．
设S△EGD=x，
∵AG=2DG，
∴S△EGA=2S△EGD=2x，
∴S△EAD=S△EGD+S△EGA=3x，
∵E为AC中点，
∴S△ECD=S△EAD=3x，
∴S△ADC=S△ECD+S△EAD=6x，
∵AD是△ABC的中线，
∴S△ABC=2S△ADC=12x，
∴S△ABC：S△CED=12x：3x=4．
故答案为4．
点评：本题考查了三角形重心的定义与性质，三角形的面积，难度适中．设S△EGD=x，用含x的代数式表示出S△ABC是解题的关键．
练习册系列答案
相关题目
若分式
有意义，则a的取值范围是（ ）
| a |
| a+1 |
| A、a≠-1 | B、a≠0 |
| C、a≠0且a≠-1 | D、任何实数 |
如图，已知直线l1∥l2，则∠a的度数为（ ）| A、115° | B、135° |
| C、145° | D、150° |
已知三角形ABC，求作三角形ABC绕点C逆时针旋转90°的三角形．（保留作图痕迹，不写作法）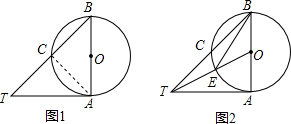
已知AB是⊙O的直径，AT与⊙O相切于点A，⊙O交BT于C，CT=CB．
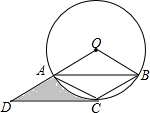如图，⊙O是△ABC的外接圆，AC=BC，CD∥AB交OA的延长线于点D．