题目内容
1. 一条公路沿线上依次有A、B、C三地.甲、乙两车同时从B地出发.匀速行驶.乙车直接驶往C地.甲车先到A地取-物品后立即调转方向追赶乙车(甲车取物品的时间忽略不计).已知两车之间的路程y(km)与甲车行驶时间x(h)的函数图象如图所示
一条公路沿线上依次有A、B、C三地.甲、乙两车同时从B地出发.匀速行驶.乙车直接驶往C地.甲车先到A地取-物品后立即调转方向追赶乙车(甲车取物品的时间忽略不计).已知两车之间的路程y(km)与甲车行驶时间x(h)的函数图象如图所示(1)求甲、乙两车的速度.
(2)A、C两地的路程是300km.图中的t=$\frac{13}{3}$
(3)求在乙车到达C地之前两车与B地距离相等时行驶的时间.
分析 (1)设甲车的速度为xkm/h,乙车的速度为ykm/h,根据函数图象上点的坐标,结合数量关系即可得出关于x、y的二元一次方程组,解方程组即可得出结论;
(2)根据函数图象找出乙车到C地的时间,以及甲车到A地的时间,依据“路程=速度×时间”分别求出A、B两地和B、C两地的路程,结合题意即可得出结论;再由“时间=路程÷速度”即可算出甲车到达C地的时间(即t);
(3)设在乙车到达C地之前两车与B地距离相等时行驶的时间为mh,根据甲、乙两车运动的过程结合数量关系即可得出关于m的一元一次方程,解方程即可得出结论.
解答 解:(1)设甲车的速度为xkm/h,乙车的速度为ykm/h,
依题意得:$\left\{\begin{array}{l}{x+y=150÷1}\\{x-y=(150-75)÷(3.5-1)}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=90}\\{y=60}\end{array}\right.$.
答:甲车的速度为90km/h,乙车的速度为60km/h.
(2)观察函数图象可知:当x=3.5时,乙车到达C地;
当x=1时,甲车到达A地.
∴A、B两地的路程为90×1=90(km),
B、C两地的路程为60×3.5=210(km),
A、C两地的路程为90+210=300(km).
甲到C地的时间为t=1+300÷90=$\frac{13}{3}$(h).
故答案为:300;$\frac{13}{3}$.
(3)设在乙车到达C地之前两车与B地距离相等时行驶的时间为mh,
依题意得:90×2-90m=60m,
解得:m=$\frac{6}{5}$.
答:在乙车到达C地之前两车与B地距离相等时行驶的时间为$\frac{6}{5}$h.
点评 本题考查了一次函数的应用、解二元一次方程组以及解一元一次方程,解题的关键是:(1)得出关于两车速度的二元一次方程组;(2)根据数量关系直接计算;(3)得出关于时间m的一元一次方程.本题属于中档题,难度不大,解决该题型题目时,结合函数图象与熟练关系得出方程(或方程)是关键.

 名校课堂系列答案
名校课堂系列答案| 年薪/万元 | 30 | 14 | 9 | 6 | 4 | 3.5 | 3 |
| 员工数/人 | 1 | 2 | 3 | 4 | 5 | 6 | 4 |
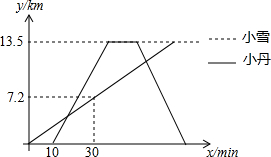 小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km.
小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km. 如图,矩形ABCD内接于⊙O,AB=2,AD=3,点P是⊙O上任一点,则sin∠APB的值为$\frac{2\sqrt{13}}{13}$.
如图,矩形ABCD内接于⊙O,AB=2,AD=3,点P是⊙O上任一点,则sin∠APB的值为$\frac{2\sqrt{13}}{13}$. 如图,在?ABCD中,BD是对角线,且DB⊥BC,E、F分别为边AB、CD的中点.求证:四边形DEBF是菱形.
如图,在?ABCD中,BD是对角线,且DB⊥BC,E、F分别为边AB、CD的中点.求证:四边形DEBF是菱形.