题目内容
将表示下列事件发生的概率的字母标在下图中:

(1)投掷一枚骰子,掷出7点的概率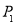 ;
;
(2)在数学测验中做一道四个选项的选择题(单选题),由于不知道那个是正确选项,现任选一个,做对的概率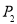 ;
;
(3)袋子中有两个红球,一个黄球,从袋子中任取一球是红球的概率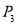 ;
;
(4)太阳每天东升西落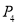 ;
;
(5)在1---100之间,随机抽出一个整数是偶数的概率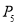 .
.
 【解析】
试题分析:(1)根据骰子没有7点,所以这种情况不可能发生,可知概率为0;
(2)选择题的答案是4选1,因此其概率为;
(3)袋子中摸到红球的概率为;
(4)太阳的东升西落是必然事件,因此其概率为1;
(5)由1---100之间有50个偶数可知随机抽取一个数为偶数的概率为.
试题解析:
【解析】
试题分析:(1)根据骰子没有7点,所以这种情况不可能发生,可知概率为0;
(2)选择题的答案是4选1,因此其概率为;
(3)袋子中摸到红球的概率为;
(4)太阳的东升西落是必然事件,因此其概率为1;
(5)由1---100之间有50个偶数可知随机抽取一个数为偶数的概率为.
试题解析:
如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB= ,则cos∠ADC= .
,则cos∠ADC= .
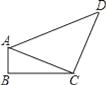
 【解析】试题分析:首先在△ABC中,根据三角函数值计算出AC=,再利用勾股定理计算出AD=10,然后根据余弦定义可算出cos∠ADC=.
【解析】试题分析:首先在△ABC中,根据三角函数值计算出AC=,再利用勾股定理计算出AD=10,然后根据余弦定义可算出cos∠ADC=. 下列说法正确的是 ( )
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形
B.一个等腰三角形一定是锐角三角形,或直角三角形
C.一个直角三角形一定不是等腰三角形,也不是等边三角形
D.一个等边三角形一定不是钝角三角形,也不是直角三角形
 D
【解析】A.一个钝角三角形不一定不是等腰三角形,不是等边三角形,故错误
B.一个等腰三角形不一定是锐角三角形,或直角三角形,故错误
C.一个直角三角形不一定不是等腰三角形,不是等边三角形,故错误
D.一个等边三角形一定不是钝角三角形,也不是直角三角形,正确
故选D
D
【解析】A.一个钝角三角形不一定不是等腰三角形,不是等边三角形,故错误
B.一个等腰三角形不一定是锐角三角形,或直角三角形,故错误
C.一个直角三角形不一定不是等腰三角形,不是等边三角形,故错误
D.一个等边三角形一定不是钝角三角形,也不是直角三角形,正确
故选D 观察如下图所示的各个图形,其中全等图形正确的是( ).
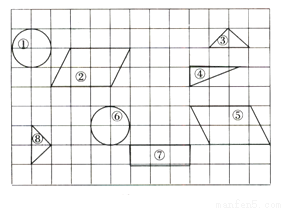
A. ②≌④ B. ⑤≌⑧ C. ①≌⑥ D. ③≌⑦
 C
【解析】观察可知 ②≌⑤,③≌⑧,①≌⑥,
故选C.
C
【解析】观察可知 ②≌⑤,③≌⑧,①≌⑥,
故选C. 下列说法正确的是( ).
A.所有正方形都是全等图形
B.面积相等的两个三角形是全等图形
C.所有半径相等的圆都是全等图形
D.所有长方形都是全等图形
 C.
【解析】
试题分析:根据全等图形的定义进行判断. A、所有正方形不一定是全等图形,故此选项错误;B、面积相等的两三角形不一定全等,故此选项错误;C、所有半径相等的圆都是全等图形,故此选项正确;D、所有长方形不一定是全等图形,故此选项错误.
故选:C.
C.
【解析】
试题分析:根据全等图形的定义进行判断. A、所有正方形不一定是全等图形,故此选项错误;B、面积相等的两三角形不一定全等,故此选项错误;C、所有半径相等的圆都是全等图形,故此选项正确;D、所有长方形不一定是全等图形,故此选项错误.
故选:C. 一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球除颜色外都相同,将球搅匀,从中任意摸出1个球.
(1)会出现哪些可能的结果? ;
(2)你认为摸到哪种颜色球的可能性最大? ;
(3)怎样改变袋子中红球和白球的个数,使摸到这两种颜色球的概率相同?
 (1)摸到红球,摸到绿球,摸到白球;(2)白球(3)放入3个红球;放入2个红球,拿走1个白球等
【解析】
试题分析:(1)由一只不透明的袋子中有2个红球、3个绿球和5个白球,即可求得答案;
(2)由一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球除颜色外都相同,即可求得摸到各种颜色球的概率,继而求得答案;
(3)使得袋子中红球和白球的个数相等即可.
【解析】
...
(1)摸到红球,摸到绿球,摸到白球;(2)白球(3)放入3个红球;放入2个红球,拿走1个白球等
【解析】
试题分析:(1)由一只不透明的袋子中有2个红球、3个绿球和5个白球,即可求得答案;
(2)由一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球除颜色外都相同,即可求得摸到各种颜色球的概率,继而求得答案;
(3)使得袋子中红球和白球的个数相等即可.
【解析】
... 如图是小鹏自己制作的正方形飞镖盘,并在盘内画了两个小正方形,则小鹏在投掷飞镖时,飞镖扎在阴影部分的概率为( )
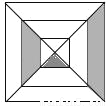
A. 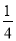 B.
B. 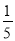 C.
C. 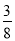 D.
D. 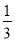
 A
【解析】根据概率公式计算可得:飞镖扎在阴影部分的概率是,故选A.
A
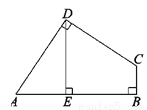
【解析】根据概率公式计算可得:飞镖扎在阴影部分的概率是,故选A. 如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DE⊥AB于点E,若四边形ABCD的面积为16,则DE=__.
 4
【解析】试题解析:过点D作BC的垂线,交BC的延长线于F,
又
∴≌,
∴,
四边形ABCD的面积=正方形DEBF的面积=16,
∴DE=4.
故答案为:4.
4
【解析】试题解析:过点D作BC的垂线,交BC的延长线于F,
又
∴≌,
∴,
四边形ABCD的面积=正方形DEBF的面积=16,
∴DE=4.
故答案为:4. 如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=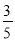 . 求:(1)点B的坐标;(2)cos∠BAO的值.
. 求:(1)点B的坐标;(2)cos∠BAO的值.
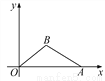
 (1)点B的坐标为(4,3);(2)cos∠BAO=.
【解析】试题分析:(1)作BH⊥OA, 垂足为H,在Rt△OHB中,根据锐角三角函数的定义及已知条件求得BH的长,再根据勾股定理求得OH的长,即可得点B的坐标;(2)先求得AH的长,在Rt△AHB中,根据勾股定理求得AB的长,根据锐角三角函数的定义即可求得cos∠BAO的值.
试题解析:
(1)如图所示,作BH⊥OA, 垂足...
(1)点B的坐标为(4,3);(2)cos∠BAO=.
【解析】试题分析:(1)作BH⊥OA, 垂足为H,在Rt△OHB中,根据锐角三角函数的定义及已知条件求得BH的长,再根据勾股定理求得OH的长,即可得点B的坐标;(2)先求得AH的长,在Rt△AHB中,根据勾股定理求得AB的长,根据锐角三角函数的定义即可求得cos∠BAO的值.
试题解析:
(1)如图所示,作BH⊥OA, 垂足... 
