题目内容
下列说法正确的是 ( )
A．一个钝角三角形一定不是等腰三角形，也不是等边三角形
B．一个等腰三角形一定是锐角三角形，或直角三角形
C．一个直角三角形一定不是等腰三角形，也不是等边三角形
D．一个等边三角形一定不是钝角三角形，也不是直角三角形
D
【解析】A．一个钝角三角形不一定不是等腰三角形，不是等边三角形,故错误
B．一个等腰三角形不一定是锐角三角形，或直角三角形，故错误
C．一个直角三角形不一定不是等腰三角形，不是等边三角形，故错误
D．一个等边三角形一定不是钝角三角形，也不是直角三角形，正确
故选D
必然事件发生的概率是________，即P(必然事件)= _______；不可能事件发生的概率是_______，即P（不可能事件）=_______；若A是不确定事件，则______＜P（A）＜______．
1 1 0 0 0 1
【解析】根据必然事件、不可能事件、不确定事件的意义，可得必然事件发生的概率是1，即P(必然事件)= 1；不可能事件发生的概率是0，即P（不可能事件）=0；若是不确定事件，则01．故答案为：(1). 必然事件发生的概率是1 (2). P(必然事件)= 1 (3). 不可能事件发生的概率是0 (4). P（不可能事件）=0 (5). 0 (6). 1 如图，△ABC中，∠B=34°，∠ACB=104°，AD是BC边上的高，AE是∠BAC的平分线，求∠DAE的度数．
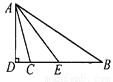
35°.
【解析】由三角形的内角和定理，可求∠BAC=70°，又由AE是∠BAC的平分线，可求∠BAE=35°，再由AD是BC边上的高，可知∠ADB=90°，可求∠BAD=25°，所以∠DAE=∠BAE-∠BAD=10°．
【解析】
在△ABC中，
∵∠BAC=180°-∠B-∠C=70°，
∵AE是∠BAC的平分线，
∴∠BAE=∠CAE=35°．
又∵AD是BC边上的高，... 如图，将一副三角板叠放在一起，使直角的顶点重合于O，则∠AOC+∠DOB=（ ）
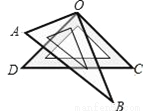
A. 90° B. 120° C. 160° D. 180°
D
【解析】设∠AOD=a,∠AOC=90°+a,∠BOD=90°?a，
所以∠AOC+∠BOD=90°+a+90°?a=180°.
故选D. 图中三角形的个数是（ ）
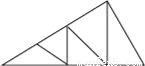
A. 8个 B. 9个 C. 10个 D. 11个
B
【解析】试题解析：∵图中的三角形有：△AGD，△ADF，△AEF，△AEC，△ABC，△DGF，△DEF，△CEF，△CEB，
∴共9个三角形.
故选B. 你能将下图分成形状相同、大小相同的12块吗？
不要满足于一种分法哦，把你的方法和其它同学交流一下，一定会有更多的收获.
见解析
【解析】试题分析：把所给图形看作是3个正方形，要分成形状、大小相同的12块，需要把每个正方形分成形状、大小相同的4块即可．
试题解析：∵要求分成全等的12块，，
∴每个小正方形要分成全等的四块. 如图△ABC，使A与D重合，则△ABC______△DBC，其对应角为_____，对应边是_______.
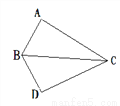
≌ ∠A=∠D，∠ABC=∠DBC；∠ACB=∠DCB AB＝DB，AC＝DC，BC＝BC.
【解析】根据题意可知△ABC≌△DBC，
所以对应角为：∠A=∠D，∠ABC=∠DBC，∠ACB=∠DCB，
对应边为：AB=DB，AC=DC，BC=BC，
故答案为：≌；∠A=∠D，∠ABC=∠DBC，∠ACB=∠DCB；AB=DB，AC=DC，BC=BC. 将表示下列事件发生的概率的字母标在下图中：
（1）投掷一枚骰子，掷出7点的概率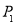
；
（2）在数学测验中做一道四个选项的选择题（单选题），由于不知道那个是正确选项，现任选一个，做对的概率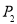
；
（3）袋子中有两个红球，一个黄球，从袋子中任取一球是红球的概率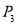
；
（4）太阳每天东升西落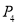
；
（5）在1---100之间，随机抽出一个整数是偶数的概率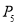
.
【解析】
试题分析：（1）根据骰子没有7点，所以这种情况不可能发生，可知概率为0；
（2）选择题的答案是4选1，因此其概率为；
（3）袋子中摸到红球的概率为；
（4）太阳的东升西落是必然事件，因此其概率为1；
（5）由1---100之间有50个偶数可知随机抽取一个数为偶数的概率为.
试题解析： 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
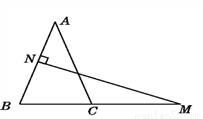
(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
(1) 20°；(2) 35°；
(3)规律:∠NMB=∠A.
【解析】（1）根据等边对等角，由AB=AC可得到∠ABM=∠ACB，再结合已知∠A的度数，即可求出∠NMB的度数；
（2）仿照第（1）问的求解过程即可得到∠NMB的度数；
（3）结合上述两问的解答，即可发现∠NMB和∠A之间的大小关系，然后仿照上述解答过程进行验证即可.
【解析】
（1）∵AB=AC，
...