题目内容
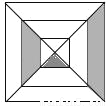
如图是小鹏自己制作的正方形飞镖盘,并在盘内画了两个小正方形,则小鹏在投掷飞镖时,飞镖扎在阴影部分的概率为( )
A. 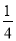 B.
B. 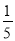 C.
C. 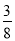 D.
D. 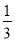
 A
【解析】根据概率公式计算可得:飞镖扎在阴影部分的概率是,故选A.
A
【解析】根据概率公式计算可得:飞镖扎在阴影部分的概率是,故选A.
如图,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
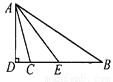
 35°.
【解析】由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=25°,所以∠DAE=∠BAE-∠BAD=10°.
【解析】
在△ABC中,
∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,...
35°.
【解析】由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=25°,所以∠DAE=∠BAE-∠BAD=10°.
【解析】
在△ABC中,
∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,... 如图△ABC,使A与D重合,则△ABC______△DBC,其对应角为_____,对应边是_______.
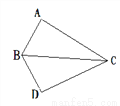
 ≌ ∠A=∠D,∠ABC=∠DBC;∠ACB=∠DCB AB=DB,AC=DC,BC=BC.
【解析】根据题意可知△ABC≌△DBC,
所以对应角为:∠A=∠D,∠ABC=∠DBC,∠ACB=∠DCB,
对应边为:AB=DB,AC=DC,BC=BC,
故答案为:≌;∠A=∠D,∠ABC=∠DBC,∠ACB=∠DCB;AB=DB,AC=DC,BC=BC.
≌ ∠A=∠D,∠ABC=∠DBC;∠ACB=∠DCB AB=DB,AC=DC,BC=BC.
【解析】根据题意可知△ABC≌△DBC,
所以对应角为:∠A=∠D,∠ABC=∠DBC,∠ACB=∠DCB,
对应边为:AB=DB,AC=DC,BC=BC,
故答案为:≌;∠A=∠D,∠ABC=∠DBC,∠ACB=∠DCB;AB=DB,AC=DC,BC=BC. 将表示下列事件发生的概率的字母标在下图中:

(1)投掷一枚骰子,掷出7点的概率 ;
;
(2)在数学测验中做一道四个选项的选择题(单选题),由于不知道那个是正确选项,现任选一个,做对的概率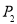 ;
;
(3)袋子中有两个红球,一个黄球,从袋子中任取一球是红球的概率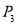 ;
;
(4)太阳每天东升西落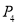 ;
;
(5)在1---100之间,随机抽出一个整数是偶数的概率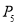 .
.
 【解析】
试题分析:(1)根据骰子没有7点,所以这种情况不可能发生,可知概率为0;
(2)选择题的答案是4选1,因此其概率为;
(3)袋子中摸到红球的概率为;
(4)太阳的东升西落是必然事件,因此其概率为1;
(5)由1---100之间有50个偶数可知随机抽取一个数为偶数的概率为.
试题解析:
【解析】
试题分析:(1)根据骰子没有7点,所以这种情况不可能发生,可知概率为0;
(2)选择题的答案是4选1,因此其概率为;
(3)袋子中摸到红球的概率为;
(4)太阳的东升西落是必然事件,因此其概率为1;
(5)由1---100之间有50个偶数可知随机抽取一个数为偶数的概率为.
试题解析: 如图,平面内有16个格点,每个格点小正方形的边长为1,则图中阴影部分的面积为__.
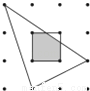
 【解析】试题解析:由题意,中间正方形中直角三角形的面积为,
∴阴影部分的面积为1-,
∴点P落在图中阴影部分的概率是.
【解析】试题解析:由题意,中间正方形中直角三角形的面积为,
∴阴影部分的面积为1-,
∴点P落在图中阴影部分的概率是. 下列事件中,属于必然事件的是( )
A.随意抛掷一枚骰子,掷得偶数点
B.从一副扑克牌抽出一张,抽得红桃牌
C.任意选择电视的某一频道,正在播放动画片
D.在同一年出生的367名学生中,至少有两个人同月同日生
 D
【解析】
试题解析:A、随意抛掷一枚骰子,掷得偶数点是随机事件,故A错误;
B、从一副扑克牌抽出一张,抽得红桃牌是随机事件,故B错误;
C、任意选择电视的某一频道,正在播放动画片是随机事件,故C错误;
D、在同一年出生的367名学生中,至少有两个人同月同日生是必然事件,故D正确;
故选D.
D
【解析】
试题解析:A、随意抛掷一枚骰子,掷得偶数点是随机事件,故A错误;
B、从一副扑克牌抽出一张,抽得红桃牌是随机事件,故B错误;
C、任意选择电视的某一频道,正在播放动画片是随机事件,故C错误;
D、在同一年出生的367名学生中,至少有两个人同月同日生是必然事件,故D正确;
故选D. 如图,房间内有一架梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,若梯子斜靠在另一面墙时,顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这个房间的宽AB是多少米?为什么?
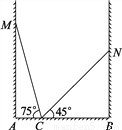
 a米.
【解析】试题分析:连结BM、MN,由SSS证明≌,可得∠CBM=∠NBM=45°,AB=AM=a.
试题解析:a米.连结BM、MN,
在△MCN中,∠MCN=180°-75°-45°=60°,CM=CN,
∴△MCN是等边三角形,
∴MC=MN,∠CBN=90°,∠BCN=45°,
∴BC=BN,在△MCB和△MNB中,
∴△MCB≌△MNB,
...
a米.
【解析】试题分析:连结BM、MN,由SSS证明≌,可得∠CBM=∠NBM=45°,AB=AM=a.
试题解析:a米.连结BM、MN,
在△MCN中,∠MCN=180°-75°-45°=60°,CM=CN,
∴△MCN是等边三角形,
∴MC=MN,∠CBN=90°,∠BCN=45°,
∴BC=BN,在△MCB和△MNB中,
∴△MCB≌△MNB,
... 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
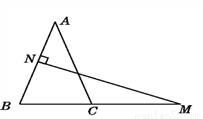
(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
 (1) 20°;(2) 35°;
(3)规律:∠NMB=∠A.
【解析】(1)根据等边对等角,由AB=AC可得到∠ABM=∠ACB,再结合已知∠A的度数,即可求出∠NMB的度数;
(2)仿照第(1)问的求解过程即可得到∠NMB的度数;
(3)结合上述两问的解答,即可发现∠NMB和∠A之间的大小关系,然后仿照上述解答过程进行验证即可.
【解析】
(1)∵AB=AC,
...
(1) 20°;(2) 35°;
(3)规律:∠NMB=∠A.
【解析】(1)根据等边对等角,由AB=AC可得到∠ABM=∠ACB,再结合已知∠A的度数,即可求出∠NMB的度数;
(2)仿照第(1)问的求解过程即可得到∠NMB的度数;
(3)结合上述两问的解答,即可发现∠NMB和∠A之间的大小关系,然后仿照上述解答过程进行验证即可.
【解析】
(1)∵AB=AC,
... 如图,直线y=2x+2与y轴交于A点,与反比例函数y=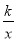 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
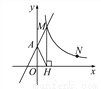
(1)求k的值;
(2)点N(a,1)是反比例函数y=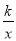 (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
 (1)4;(2)P(,0)
【解析】试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.
(1)4;(2)P(,0)
【解析】试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置. 
