题目内容
如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB= ,则cos∠ADC= .
,则cos∠ADC= .
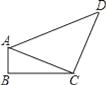
 【解析】试题分析:首先在△ABC中,根据三角函数值计算出AC=,再利用勾股定理计算出AD=10,然后根据余弦定义可算出cos∠ADC=.
【解析】试题分析:首先在△ABC中,根据三角函数值计算出AC=,再利用勾股定理计算出AD=10,然后根据余弦定义可算出cos∠ADC=.
若x、y表示有理数,则下列各数中一定是正数的是( )
A. 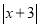 B.
B. 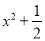 C.
C. 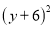 D.
D. 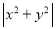
 B
【解析】试题分析:A、|x+3|≥0,故此选项错误;
B、x2≥0,x2+≥>0,故此选项正确;
C、(y+6)2≥0,故此选项错误;
D、|x2+y2|≥0,故此选项错误.
故选B.
B
【解析】试题分析:A、|x+3|≥0,故此选项错误;
B、x2≥0,x2+≥>0,故此选项正确;
C、(y+6)2≥0,故此选项错误;
D、|x2+y2|≥0,故此选项错误.
故选B. 必然事件发生的概率是________,即P(必然事件)= _______;不可能事件发生的概率是_______,即P(不可能事件)=_______;若A是不确定事件,则______<P(A)<______.
 1 1 0 0 0 1
【解析】根据必然事件、不可能事件、不确定事件的意义,可得必然事件发生的概率是1,即P(必然事件)= 1;不可能事件发生的概率是0,即P(不可能事件)=0;若是不确定事件,则01.故答案为:(1). 必然事件发生的概率是1 (2). P(必然事件)= 1 (3). 不可能事件发生的概率是0 (4). P(不可能事件)=0 (5). 0 (6). 1
1 1 0 0 0 1
【解析】根据必然事件、不可能事件、不确定事件的意义,可得必然事件发生的概率是1,即P(必然事件)= 1;不可能事件发生的概率是0,即P(不可能事件)=0;若是不确定事件,则01.故答案为:(1). 必然事件发生的概率是1 (2). P(必然事件)= 1 (3). 不可能事件发生的概率是0 (4). P(不可能事件)=0 (5). 0 (6). 1 学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.( 取1.732,结果保留整数)
取1.732,结果保留整数)
 411米.
【解析】试题分析:首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造边角关系,进而可求出答案.
试题解析:设AH=x米,在Rt△EHG中,∵∠EGH=45°,∴GH=EH=AE+AH=x+12,∵GF=CD=288米,∴HF=GH+GF=x+12+288=x+300,在Rt△AHF中,∵∠AFH=30°,∴AH=HF•tan∠AFH,即x=(x...
411米.
【解析】试题分析:首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造边角关系,进而可求出答案.
试题解析:设AH=x米,在Rt△EHG中,∵∠EGH=45°,∴GH=EH=AE+AH=x+12,∵GF=CD=288米,∴HF=GH+GF=x+12+288=x+300,在Rt△AHF中,∵∠AFH=30°,∴AH=HF•tan∠AFH,即x=(x... 在Rt△ABC中,∠C=90°,a=8,∠B=60°,解这个直角三角形.
 ∠A=30°,AB=16,AC=
【解析】试题分析:根据三角形内角和定理求出∠A,根据含30度角直角三角形求出AB,根据勾股定理求出AC即可.
试题解析:∵∠C=90°,∠B=60°,
∴∠A=180°-∠C-∠B=30°,
∵BC=a=8,
∴AB=2a=16,
由勾股定理得:AC= .
∠A=30°,AB=16,AC=
【解析】试题分析:根据三角形内角和定理求出∠A,根据含30度角直角三角形求出AB,根据勾股定理求出AC即可.
试题解析:∵∠C=90°,∠B=60°,
∴∠A=180°-∠C-∠B=30°,
∵BC=a=8,
∴AB=2a=16,
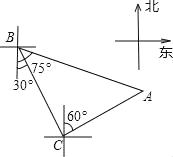
由勾股定理得:AC= . 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
A.25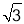 B.25
B.25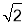 C.50 D.25
C.50 D.25
 D.
【解析】
试题分析:根据题中所给信息,求出∠BCA=90°,再求出∠CBA=45°,从而得到△ABC为等腰直角三角形,然后根据解直角三角形的知识解答.如图:根据题意,∠1=∠2=30°,∵∠ACD=60°,∴∠ACB=30°+60°=90°,∴∠CBA=75°﹣30°=45°,∴△ABC为等腰直角三角形,∵BC=50×0.5=25,∴AC=BC=25(海里).故选D.
D.
【解析】
试题分析:根据题中所给信息,求出∠BCA=90°,再求出∠CBA=45°,从而得到△ABC为等腰直角三角形,然后根据解直角三角形的知识解答.如图:根据题意,∠1=∠2=30°,∵∠ACD=60°,∴∠ACB=30°+60°=90°,∴∠CBA=75°﹣30°=45°,∴△ABC为等腰直角三角形,∵BC=50×0.5=25,∴AC=BC=25(海里).故选D. 如图,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
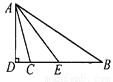
 35°.
【解析】由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=25°,所以∠DAE=∠BAE-∠BAD=10°.
【解析】
在△ABC中,
∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,...
35°.
【解析】由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=25°,所以∠DAE=∠BAE-∠BAD=10°.
【解析】
在△ABC中,
∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,... 如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=( )
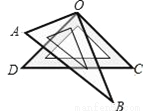
A. 90° B. 120° C. 160° D. 180°
 D
【解析】设∠AOD=a,∠AOC=90°+a,∠BOD=90°?a,
所以∠AOC+∠BOD=90°+a+90°?a=180°.
故选D.
D
【解析】设∠AOD=a,∠AOC=90°+a,∠BOD=90°?a,
所以∠AOC+∠BOD=90°+a+90°?a=180°.
故选D. 将表示下列事件发生的概率的字母标在下图中:

(1)投掷一枚骰子,掷出7点的概率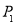 ;
;
(2)在数学测验中做一道四个选项的选择题(单选题),由于不知道那个是正确选项,现任选一个,做对的概率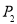 ;
;
(3)袋子中有两个红球,一个黄球,从袋子中任取一球是红球的概率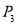 ;
;
(4)太阳每天东升西落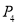 ;
;
(5)在1---100之间,随机抽出一个整数是偶数的概率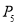 .
.
 【解析】
试题分析:(1)根据骰子没有7点,所以这种情况不可能发生,可知概率为0;
(2)选择题的答案是4选1,因此其概率为;
(3)袋子中摸到红球的概率为;
(4)太阳的东升西落是必然事件,因此其概率为1;
(5)由1---100之间有50个偶数可知随机抽取一个数为偶数的概率为.
试题解析:
【解析】
试题分析:(1)根据骰子没有7点,所以这种情况不可能发生,可知概率为0;
(2)选择题的答案是4选1,因此其概率为;
(3)袋子中摸到红球的概率为;
(4)太阳的东升西落是必然事件,因此其概率为1;
(5)由1---100之间有50个偶数可知随机抽取一个数为偶数的概率为.
试题解析: 
