题目内容
6.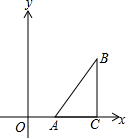 如图:Rt△ACB中,∠C=90°;△ACB的边AC在x轴正半轴上,AC=2OA.已知Rt△ACB面积是4.求经过点B反比例函数的解析式.
如图:Rt△ACB中,∠C=90°;△ACB的边AC在x轴正半轴上,AC=2OA.已知Rt△ACB面积是4.求经过点B反比例函数的解析式.
分析 连接OB,设B(m,n)(m>0,n>0),则有△ABC的面积为$\frac{1}{2}×AC×BC=4$,由AC=2OA,得出△ABO的面积为2,得出△CBO的面积=$\frac{1}{2}×OC×BC$=$\frac{1}{2}$mn=6,得出mn=12,从而求得反比例函数系数k=12,即可得出反比例函数的解析式.
解答 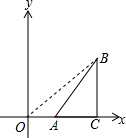 解:如图:连接OB,设B(m,n)(m>0,n>0)则有△ABC的面积为$\frac{1}{2}×AC×BC=4$;
解:如图:连接OB,设B(m,n)(m>0,n>0)则有△ABC的面积为$\frac{1}{2}×AC×BC=4$;
∵△ABO的面积为$\frac{1}{2}×AO×BC$,AC=2OA,
∴△ABO的面积为$\frac{1}{2}×\frac{1}{2}×AC×BC=\frac{1}{4}×AC×BC$=2
∴△CBO的面积为2+4=6
∴△CBO的面积=$\frac{1}{2}×OC×BC$=$\frac{1}{2}$mn=6,
∴mn=12
设经过点B的反比例函数的解析式为$y=\frac{k}{x}$(k≠0)
∵k=mn=12,
∴经过点B反比例函数的解析式为$y=\frac{12}{x}$.
点评 本题考查了待定系数法求反比例函数的解析式和反比例函数系数k的几何意义,由△CBO的面积=$\frac{1}{2}$mn=6,求得系数k的值是解题的关键.

练习册系列答案
相关题目
16.若式子$\frac{\sqrt{x-1}}{x+2}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥1且x≠0 | B. | x>1 且x≠-2 | C. | x≥1 | D. | x≥1 且x≠-2 |
11.若满足方程组$\left\{\begin{array}{l}{3x+2y=2a+1}\\{2x+3y=a-1}\end{array}\right.$的x-y的值是2,则a的值是( )
| A. | 2 | B. | 4 | C. | 0 | D. | 不确定 |
18.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. | 等边三角形 | B. | 圆 | C. | 矩形 | D. | 平行四边形 |
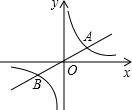 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4.
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4.