题目内容
1.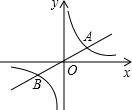 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4.
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4.(1)求k的值;
(2)若双曲线y=$\frac{k}{x}$(k>0)上一点C的纵坐标为8,求△AOC的面积;
(3)根据图象写出使一次函数值大于反比例函数值的x的取值范围.
分析 (1)将x=4代入一次函数解析式求出y的值,确定出A的坐标,将A坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;
(2)将C纵坐标代入反比例解析式求出横坐标,确定出C坐标,即CD与OD的长,三角形AAOC面积=三角形COD面积+梯形AEDC面积-三角形AOE面积,求出即可;
(3)根据A的坐标求得B的坐标,然后根据图象即可求得.
解答 解:(1)将x=4代入y=$\frac{1}{2}$x=2,即A(4,2),
将A(4,2)代入反比例解析式得:k=8;
(2)过C作CD⊥x轴,作AE⊥x轴,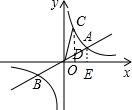 将y=8代入反比例解析式得:x=1,即C(1,8),
将y=8代入反比例解析式得:x=1,即C(1,8),
∴OD=1,CD=8,
∵A(4,2),
∴OE=4,AE=2,
∵S△AOC=S△COD+S梯形AEDC-S△AOE=$\frac{1}{2}$×1×8+$\frac{1}{2}$×(2+8)×3-$\frac{1}{2}$×4×2=15;
(3)∵A(4,2),
∴B(-4,2),
由图象可知:一次函数值大于反比例函数值的x的取值范围是x>4或-4<x<0.
点评 此题考查了反比例函数和一次函数的交点问题,其知识点有:坐标与图形性质,三角形、梯形的面积,以及待定系数法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
 如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )| A. | 32 | B. | 24 | C. | 40 | D. | 20 |
9.下列各式中,是完全平方式的是( )
| A. | m2-m+1 | B. | x2-18x+9 | C. | a2+2ab-b2 | D. | t2-t+$\frac{1}{4}$ |
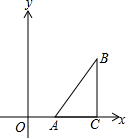 如图:Rt△ACB中,∠C=90°;△ACB的边AC在x轴正半轴上,AC=2OA.已知Rt△ACB面积是4.求经过点B反比例函数的解析式.
如图:Rt△ACB中,∠C=90°;△ACB的边AC在x轴正半轴上,AC=2OA.已知Rt△ACB面积是4.求经过点B反比例函数的解析式.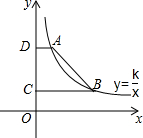 如图,点A(2,6),B在反比例函数y=$\frac{k}{x}$(x>0)的图象上,AD⊥y轴于点D,BC⊥y轴于点C,DC=4.
如图,点A(2,6),B在反比例函数y=$\frac{k}{x}$(x>0)的图象上,AD⊥y轴于点D,BC⊥y轴于点C,DC=4. 如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是48cm,求:
如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是48cm,求: