题目内容
17.(1)计算:|$\sqrt{2}$|+($\frac{1}{4}$)-1-2cos45°(2)解不等式组$\left\{\begin{array}{l}{x≥\frac{x-1}{2}}\\{1+3(x-1)<6-x}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)运用特殊角的三角函数值及负整数指数幂和绝对值的运算法则运算即可;
(2)求出两个不等式的解集,根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:(1)原式=$\sqrt{2}+4-\sqrt{2}$
=4
(2)解不等式组$\left\{\begin{array}{l}{x≥\frac{x-1}{2}}\\{1+3(x-1)<6-x}\end{array}\right.$
解不等式x$≥\frac{x-1}{2}$得:x≥1,
解不等式1+3(x-1)<6-x得:x<2
在同一数轴上表示两个不等式解集如下:
∴原不等式组的解集为:-1≤x<2.
点评 本题考查了特殊角的三角函数值及负整数指数幂和绝对值的运算以及解一元一次不等式组,解此题的关键是能熟练掌握运算法则,根据不等式的解集找出不等式组的解集.

练习册系列答案
相关题目
16.对于函数y=-$\frac{3}{x}$,当x<0时,函数图象位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
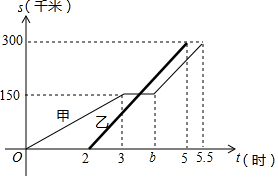 甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.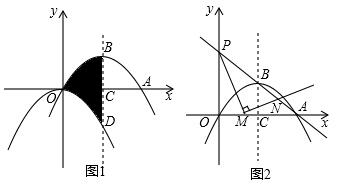
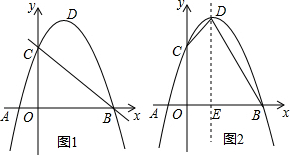 如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、点B(点A在点B左侧),与y轴交于点C,点D为抛物线的顶点,已知点A、点B的坐标分别为A(-1,0)、B(3,0).
如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、点B(点A在点B左侧),与y轴交于点C,点D为抛物线的顶点,已知点A、点B的坐标分别为A(-1,0)、B(3,0). 设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.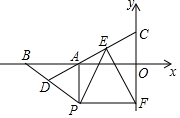 已知:如图,平面直角坐标系中,点B坐标为(-4,0),点A为线段OB中点,点P在第三象限,且AP⊥y轴,PF⊥y轴,D为BP中点,连接DA并延长交y轴于点C,FE⊥DC.
已知:如图,平面直角坐标系中,点B坐标为(-4,0),点A为线段OB中点,点P在第三象限,且AP⊥y轴,PF⊥y轴,D为BP中点,连接DA并延长交y轴于点C,FE⊥DC.