题目内容
13.1)计算:$\sqrt{2}$+$(\frac{1}{2})^{-2}$+(-1)0-2sin45°2)求满足$\left\{\begin{array}{l}{2x+y=15}\\{y+7x≤22}\end{array}$ 的x、y的正整数解.
分析 (1)涉及零指数幂、负指数幂、特殊角的三角函数值3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
(2)首先给出x的正整数值,进而求得对应的y的值,进行判断即可.
解答 解:(1)原式=$\sqrt{2}$+4+1-2×$\frac{\sqrt{2}}{2}$=5.
(2)由2x+y=15可知y=15-2x,
代入y+7x≤22得,15-2x+7x≤22,
解得x≤$\frac{7}{5}$,
当x=1时,代入2x+y=15,解得y=13,
所以满足$\left\{\begin{array}{l}{2x+y=15}\\{y+7x≤22}\end{array}$ 的x、y的正整数解是$\left\{\begin{array}{l}{x=1}\\{y=13}\end{array}\right.$.
点评 此题考查实数的综合运算能力,不等式组的整数解,对所求的数进行判断是关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1. 如图,AB为⊙O直径,点C,D为⊙O上两点,若∠C+∠AOD=145°,则∠C的大小是( )
如图,AB为⊙O直径,点C,D为⊙O上两点,若∠C+∠AOD=145°,则∠C的大小是( )
 如图,AB为⊙O直径,点C,D为⊙O上两点,若∠C+∠AOD=145°,则∠C的大小是( )
如图,AB为⊙O直径,点C,D为⊙O上两点,若∠C+∠AOD=145°,则∠C的大小是( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
18.下列运算正确的是( )
| A. | x2+x3=x5 | B. | (x-2)2=x2-4 | C. | (x3)4=x7 | D. | 2x2?x3=2x5 |
 如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,-1).
如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,-1).
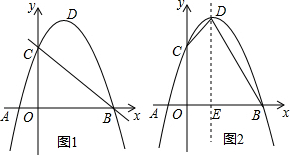 如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、点B(点A在点B左侧),与y轴交于点C,点D为抛物线的顶点,已知点A、点B的坐标分别为A(-1,0)、B(3,0).
如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、点B(点A在点B左侧),与y轴交于点C,点D为抛物线的顶点,已知点A、点B的坐标分别为A(-1,0)、B(3,0).