��Ŀ����
2����ͼ��������y=-x2+bx+c��ֱ��y=mx+n�ཻ�ڵ�A��1��8���͵�B��5��4������1���������ߺ�ֱ��AB�Ľ���ʽ��
��2����ͼ1��ֱ��AB�Ϸ�������������һ��P������P��PQ��ֱ��AB����ֱ�ߣ�����ΪQ����x���������y���������Ϸֱ�����������M��N������PN��NM��MB��BP�����߶�PQ�ij������ʱ�����ı���PNMB�ܳ�����Сֵ��
��3����ͼ2����������y�ύ�ڵ�C��ֱ��AB��x���ڵ�E����D��$\frac{4\sqrt{3}}{3}$��0��������CD����CD���ڵ�ֱ�����ŵ�D˳ʱ����ת90�㣬����ֱ�߽�ֱ��AB�ڵ�H����ֱ��DH����x��������ƽ�Ƶõ�ֱ��D1H1�����е�H1Ϊֱ��D1H1��ֱ��AB�Ľ��㣬D1Ϊֱ��D1H1��x��Ľ��㣬����D1ƽ�Ƶ���Eʱƽ�ƽ���������BD1������BD1H1�ǵ���������ʱ���������D1�����꣮

���� ��1���ѵ�A��1��8���͵�B��5��4������������y=-x2+bx+c��ֱ��y=mx+n�Ľ���ʽ���ɽ�����⣮
��2����ͼ1�У���ֱ��AB��x�ύ�ڵ�F����y�ύ�ڵ�E����E��0��9����F��9��0��������PE��PF��PO����PQ���ʱ����PEF����������P��m��-m2+5m+4��
�������κ�����ȷ����P���꣬����P����y��ĶԳƵ�P�䣬B����x��ĶԳƵ�B�䣬����P��B����y�ύ�ڵ�N����x�ύ�ڵ�M����ʱ�ı���PNMB���ܳ���С��
��3���������������ۢٵ�D1B=D1H1ʱ����BN��x����N����ֱ�������Ρ�BD1N���ɣ��ڵ�BD1=BH1ʱ����ͼ3�У���BN��DE��N����Ϊ��NBD1=15�㣬BN=4���ѡ�BND1�Ŵ�õ�ͼ4����BN��ȡһ��M��ʹ��BM=MD1�����MBD1=��MD1B=15�㣬��NMD1=30�㣬��ND1=a����MD1=MB=2a��MN=$\sqrt{3}$a��BD1=$\sqrt{{a}^{2}+��2a+\sqrt{3}a��^{2}}$=��$\sqrt{6}$+$\sqrt{2}$��a���г����̼��ɽ�����⣻�۵�H1B=H1Dʱ����ͼ5�У��ɡ�D1BN=7.5�㣬�ѡ�BD1N�Ŵ���ͼ6�У���BN�Ͻ�ȡBM=MD1��KM=KD1����ND1=a���ɢڿ�֪��MK=KD1=2a��KN=$\sqrt{3}$a��BM=MD1=��$\sqrt{6}$+$\sqrt{2}$��a���г����̼��ɽ�����⣮
��� �⣺��1����������y=-x2+bx+c��ֱ��y=mx+n�ཻ�ڵ�A��1��8���͵�B��5��4����
��$\left\{\begin{array}{l}{-1+b+c=8}\\{-25+5b+c=4}\end{array}\right.$��$\left\{\begin{array}{l}{m+n=8}\\{5m+n=4}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=5}\\{c=4}\end{array}\right.$��$\left\{\begin{array}{l}{m=-1}\\{n=9}\end{array}\right.$��
�������߽���ʽΪy=-x2+5x+4��ֱ��y����ʽΪ=-x+9��
��2����ͼ1�У���ֱ��AB��x�ύ�ڵ�F����y�ύ�ڵ�E����E��0��9����F��9��0��������PE��PF��PO��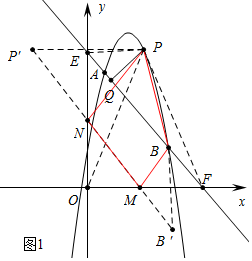
��PQ���ʱ����PEF����������P��m��-m2+5m+4��
��S��PEF=S��POE+S��POF-S��EOF=$\frac{1}{2}$��9��m+$\frac{1}{2}$��9����-m2+5m+4��-$\frac{1}{2}$��9��9=-$\frac{9}{2}$��m-3��2+18��
��-$\frac{9}{2}$��0��
��m=3ʱ����PEF��������ֵΪ18����ʱP��3��10����
����P����y��ĶԳƵ�P�䣬B����x��ĶԳƵ�B�䣬����P��B����y�ύ�ڵ�N����x�ύ�ڵ�M����ʱ�ı���PNMB���ܳ���С��
���ɣ��ı���PNMB�ܳ�=PN+MN+MB+PB=P��N+MN+MB��+PB=P��B��+PB��
��PB�Ƕ���������֮���߶���̣�
���ʱ�ı���PNMB�ܳ���С��
��P�䣨-3��10����B�䣨5��-4����
��P��B��=$\sqrt{{8}^{2}+1{4}^{2}}$=2$\sqrt{65}$��
��PB=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$��
���ı���PNMB�ܳ�����СֵΪ2$\sqrt{65}$+2$\sqrt{10}$��
��3����ͼ2�У�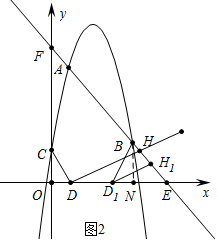
��C��0��4����D��$\frac{4\sqrt{3}}{3}$����
��OC=4��OD=$\frac{4\sqrt{3}}{3}$��
��tan��ODC=$\frac{OC}{OD}$=$\sqrt{3}$��
���CDO=60�㣬
��CD��DH��
���HDE=30�㣬
��OF=OF��
���OFE=��OEF=45�㣬
���AHD=��BH1D1=75�㣬
�ٵ�D1B=D1H1ʱ����BN��x����N��
�ߡ�D1BH1=��D1H1B=75�㣬
���BD1H1=30�㣬
��D1H1��DH��
���EDH=��ED1H1=30�㣬
���BD1N=60�㣬
��Rt��BD1N�У���D1N=NB•tan30�㣬
��D1N=$\frac{4\sqrt{3}}{3}$��
��ON=5
��OD1=5-$\frac{4\sqrt{3}}{3}$��
��D1������5-$\frac{4\sqrt{3}}{3}$��0����
�ڵ�BD1=BH1ʱ����ͼ3�У���BN��DE��N��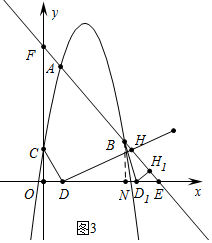
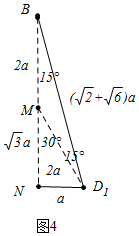
�ߡ�NBD1=15�㣬BN=4���ѡ�BND1�Ŵ�õ�ͼ4��
��BN��ȡһ��M��ʹ��BM=MD1�����MBD1=��MD1B=15�㣬��NMD1=30�㣬
��ND1=a����MD1=MB=2a��MN=$\sqrt{3}$a��BD1=$\sqrt{{a}^{2}+��2a+\sqrt{3}a��^{2}}$=��$\sqrt{6}$+$\sqrt{2}$��a�������������
��2a+$\sqrt{3}$a=4��
��a=4��2-$\sqrt{3}$��M
��OD1=5+4��2-$\sqrt{3}$��=13-4$\sqrt{3}$��
��D1������13-4$\sqrt{3}$��0����
�۵�H1B=H1Dʱ����ͼ5�У�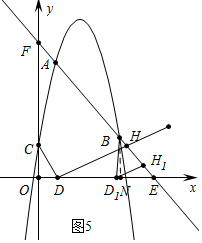
�ߡ�H1BD1=��H1D1B=$\frac{1}{2}$��180��-75�㣩=52.5�㣬��NHE=45�㣬
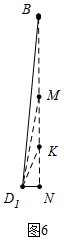
���D1BN=7.5�㣬�ѡ�BD1N�Ŵ���ͼ6�У�
��BN�Ͻ�ȡBM=MD1��KM=KD1����ND1=a��
�ɢڿ�֪��MK=KD1=2a��KN=$\sqrt{3}$a��BM=MD1=��$\sqrt{6}$+$\sqrt{2}$��a��
��$\sqrt{3}$a+2a+��$\sqrt{6}$+$\sqrt{2}$��a=4��
��a=$\frac{4}{\sqrt{6}+\sqrt{3}+\sqrt{2}+2}$��
��OD1=5-$\frac{4}{\sqrt{6}+\sqrt{3}+\sqrt{2}+2}$��
��D1������5-$\frac{4}{\sqrt{6}+\sqrt{3}+\sqrt{2}+2}$��0����
��������������BD1H1�ǵ���������ʱ��D1������Ϊ��5-$\frac{4\sqrt{3}}{3}$��0����13-4$\sqrt{3}$��0����5-$\frac{4}{\sqrt{6}+\sqrt{3}+\sqrt{2}+2}$��0����
���� ���⿼����κ����ۺ��⡢��Сֵ���⡢���������ε����ʺ��ж���������Ǻ�����֪ʶ������Ĺؼ���ѧ����ת����˼��˼�����⣬ѧ�����öԳƽ����Сֵ���⣬ѧ�ṹ�����κ��������ֵ���⣬ѧ��������ۣ�ע��15�Ƚǻ�7.5�ȵ�ת�������������п�ѹ���⣮

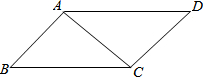 ��֪����ͼ��AB��AC��DC��AC��AD=BC�������HL�������ɵá�ABC�ա�CDA��
��֪����ͼ��AB��AC��DC��AC��AD=BC�������HL�������ɵá�ABC�ա�CDA��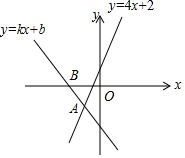 ��ͼ��ֱ��y=kx+b��ֱ��y=4x+2�ཻ�ڵ�A��-1��-2������ʽ��k-4��x��2-b�Ľ⼯Ϊx��-1��
��ͼ��ֱ��y=kx+b��ֱ��y=4x+2�ཻ�ڵ�A��-1��-2������ʽ��k-4��x��2-b�Ľ⼯Ϊx��-1�� ��ͼ���ڡ�ABC�У�AB=AC=10cm��DE��AB�Ĵ�ֱƽ���ߣ��ֱ�AB��AC��D��E���㣮��BC=6cm�����BCE���ܳ���16 cm��
��ͼ���ڡ�ABC�У�AB=AC=10cm��DE��AB�Ĵ�ֱƽ���ߣ��ֱ�AB��AC��D��E���㣮��BC=6cm�����BCE���ܳ���16 cm��