题目内容
3.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,表是试验中的一组统计数据:| 摸球的 次数n | 100 | 200 | 300 | 500 | 800 | 1 000 | 2 000 |
| 摸到白球 的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1 202 |
| 摸到白球的频率$\frac{m}{n}$ | 0.650 | 0.620 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率约为0.6.
分析 (1)计算出其平均值即可;
(2)概率接近于(1)得到的频率;
解答 解:(1)∵摸到白球的频率为(0.65+0.62+0.593+0.604+0.601+0.599+0.601)÷7≈0.6,
∴当n很大时,摸到白球的频率将会接近0.6.
(2)∵摸到白球的频率为0.6,
∴假如你摸一次,你摸到白球的概率P(白球)=0.6.
故答案为:0.6,0.6.
点评 本题比较容易,考查利用频率估计概率.大量反复试验下频率稳定值即概率.用到的知识点为:部分的具体数目=总体数目×相应频率.

练习册系列答案
相关题目
18.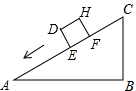 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=( )米时,有DC2=AE2+BC2.
一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=( )米时,有DC2=AE2+BC2.
 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=( )米时,有DC2=AE2+BC2.
一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=( )米时,有DC2=AE2+BC2.| A. | $\frac{14}{3}$ | B. | $\frac{16}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{2}$ |
13.计算-5a5b3c÷(15a4b3)的结果是( )
| A. | 3ac | B. | -3ac | C. | $\frac{1}{3}$ac | D. | -$\frac{1}{3}$ac |