题目内容
5.若a-3是一个数的算术平方根,则( )| A. | a≥0 | B. | a≥3 | C. | a>0 | D. | a>3 |
分析 根据算术平方根的定义即可列出不等式求出a的范围
解答 解:一个非负数才有算术平方根,且该数的算术平方根大于或等于0
∴a-3≥0
故选(B)
点评 本题考查算术平方根的性质,解题的关键是正确理解算术平方根的概念,本题属于基础题型.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
16.如图,这些几何体都是简单几何体,请你仔细观察.
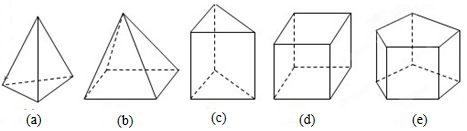
(1)认真统计每个几何体的棱数(E)、面数(F)、顶点数(V),完成表.
(2)观察表,不难发现:
①简单几何体中,每条棱都是2个面的公共边;
②在几何体c、d、e中,每个顶点处有3条棱,每条棱都有2个顶点,所以有2×E=3×V;
③简单几何体中,V、F、E之间满足后面的关系式:V+F-E=2.
(3)应用(2)题结论解答:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.则它共有30条棱,共有20个顶点,每个顶点处有3条棱.
(4)将(3)题的解题过程简要叙述在后面.

(1)认真统计每个几何体的棱数(E)、面数(F)、顶点数(V),完成表.
| 几何体 | a | b | c | d | e |
| 棱数(E) | 6 | 8 | 9 | 12 | 15 |
| 面数(F) | 4 | 5 | 5 | 6 | 7 |
| 顶点数(V) | 4 | 5 | 6 | 8 | 10 |
①简单几何体中,每条棱都是2个面的公共边;
②在几何体c、d、e中,每个顶点处有3条棱,每条棱都有2个顶点,所以有2×E=3×V;
③简单几何体中,V、F、E之间满足后面的关系式:V+F-E=2.
(3)应用(2)题结论解答:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.则它共有30条棱,共有20个顶点,每个顶点处有3条棱.
(4)将(3)题的解题过程简要叙述在后面.
20.下列一元二次方程有两个相等实数根的是( )
| A. | 2x2-x-1=0 | B. | x2-4x+4=0 | C. | 4x2-2x-3=0 | D. | x2+6x=0 |
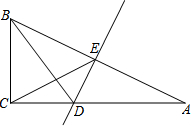 如图,在Rt△ABC中,∠C=Rt∠,AB的垂直平分线交AC于点D,交AB于点E,BD平分∠ABC.
如图,在Rt△ABC中,∠C=Rt∠,AB的垂直平分线交AC于点D,交AB于点E,BD平分∠ABC. 某中学的铅球场如图所示,已知扇形OAB的面积是72π米2,弧AB的长度为6π米,那么圆心角为45度.
某中学的铅球场如图所示,已知扇形OAB的面积是72π米2,弧AB的长度为6π米,那么圆心角为45度.