题目内容
10.我们知道:$\sqrt{3}$是一个无理数,它是无限不循环小数,且1<$\sqrt{3}$<2,则我们把1叫做$\sqrt{3}$的整数部分,$\sqrt{3}$-1叫做$\sqrt{3}$的小数部分.如果$\root{3}{50}$的整数部分为a,小数部分为b,求代数式(a+b)3的值.分析 先依据立方根的性质估算出$\root{3}{50}$的大小,然后可求得a,b的值,最后代入计算即可.
解答 解:∵27<50<64,
∴3<$\root{3}{50}$<4,
∴$\root{3}{50}$的整数部分a=3,小数部分b=$\root{3}{50}$-3.
∴(a+b)3=(3+$\root{3}{50}$-3)3=($\root{3}{50}$)3=50.
点评 本题主要考查的是估算无理数的大小,依据立方根的性质求得a,b的值是解题的关键.

练习册系列答案
相关题目
5.若a-3是一个数的算术平方根,则( )
| A. | a≥0 | B. | a≥3 | C. | a>0 | D. | a>3 |
2.下列计算正确的是( )
| A. | 2a-a=2 | B. | x3+x3=x6 | C. | a2•b2=(ab)4 | D. | 2t2+t2=3t2 |
19.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
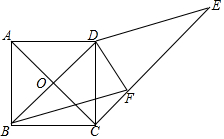 如图,正方形ABCD的边长为1,对角线交于点O,作∠DBF=30°,CE∥BD,DE∥BF,CE与BF交于点F,连接DF,∠DFC=105°.
如图,正方形ABCD的边长为1,对角线交于点O,作∠DBF=30°,CE∥BD,DE∥BF,CE与BF交于点F,连接DF,∠DFC=105°.