题目内容
16.如图,这些几何体都是简单几何体,请你仔细观察.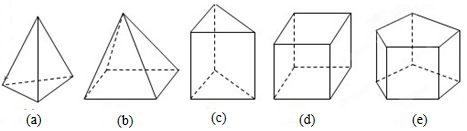
(1)认真统计每个几何体的棱数(E)、面数(F)、顶点数(V),完成表.
| 几何体 | a | b | c | d | e |
| 棱数(E) | 6 | 8 | 9 | 12 | 15 |
| 面数(F) | 4 | 5 | 5 | 6 | 7 |
| 顶点数(V) | 4 | 5 | 6 | 8 | 10 |
①简单几何体中,每条棱都是2个面的公共边;
②在几何体c、d、e中,每个顶点处有3条棱,每条棱都有2个顶点,所以有2×E=3×V;
③简单几何体中,V、F、E之间满足后面的关系式:V+F-E=2.
(3)应用(2)题结论解答:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.则它共有30条棱,共有20个顶点,每个顶点处有3条棱.
(4)将(3)题的解题过程简要叙述在后面.
分析 (1)根据观察图形可得;
(2)根据顶点与棱的关系,可得答案;
(3)根据正十二边形有十二个面,每个面是五边形,每条棱为两个面共用,可得楞数,再根据棱与顶点的关系,可得顶点数;
(4)利用(3)中所得结论解答.
解答 解:(1)如下所示:
| 几何体 | a | b | c | d | e |
| 棱数(E) | 6 | 8 | 9 | 12 | 15 |
| 面数(F) | 4 | 5 | 5 | 6 | 7 |
| 顶点数(V) | 4 | 5 | 6 | 8 | 10 |
②在几何体c、d、e中,每个顶点处有3条棱,每条棱都有2个顶点,所以有2×E=3×V;
③简单几何体中,V、F、E之间满足后面的关系式:V+F-E=2;
故答案为:①2;②3,2;③2;
(3)有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.则它有30条棱,20个顶点,每个顶点处有3条棱;
故答案为:30,20,3;
(4)正十二面体的棱数E=30、顶点数V=20和面数F=12满足:20+12-2=30,即V+F-2=E.
点评 本题考查了欧拉公式,顶点数+面数-棱数=2,注意2×E=3×V.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
4.若(am+1bn+2)•(-a2n-1b2m)=-a3b5,则m+n的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | -3 |
5.若a-3是一个数的算术平方根,则( )
| A. | a≥0 | B. | a≥3 | C. | a>0 | D. | a>3 |
6.用科学记数法表示数0.000 000 2016正确的是( )
| A. | 20.16×10-8 | B. | 2.016×10-6 | C. | 2.016×107 | D. | 2.016×10-7 |