题目内容
9.已知:先化简,再求值:$\frac{{{a^2}+ab}}{{{a^2}+2ab+{b^2}}}$-(a-b)÷$\frac{{{a^2}-{b^2}}}{b}$,其中a=2+$\sqrt{2}$,b=2-$\sqrt{2}$.分析 先将原式化简,然后将a与b代入即可求出答案.
解答 解:当a=2+$\sqrt{2}$,b=2-$\sqrt{2}$
原式=$\frac{a(a+b)}{(a+b)^{2}}$-(a-b)×$\frac{b}{(a-b)(a+b)}$
=$\frac{a}{a+b}$-$\frac{b}{a+b}$
=$\frac{a-b}{a+b}$
=$\frac{2\sqrt{2}}{4}$
=$\frac{\sqrt{2}}{2}$
点评 本题考查分式的化简求值,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
14.已知关于x 的分式方程$\frac{a+2}{x+1}$=1的解是非正数,则a的取值范围是( )
| A. | a≤-1且a≠-2 | B. | a≤-1 | C. | a≤1且a≠-2 | D. | a≤1 |
1.下列根式中属最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{4a+4}$ |
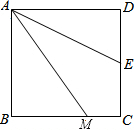 如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM.
如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM. 如图,边长为5的正方形ABCD中,CE=DF,若DG2+GE2=29,则CF的长为3.
如图,边长为5的正方形ABCD中,CE=DF,若DG2+GE2=29,则CF的长为3. 如图,△ABC中,AD⊥BC于D,点E在CD上,则图中以AD为高的三角形有6个.
如图,△ABC中,AD⊥BC于D,点E在CD上,则图中以AD为高的三角形有6个. 如图,在?ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
如图,在?ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.