题目内容
17. 如图,边长为5的正方形ABCD中,CE=DF,若DG2+GE2=29,则CF的长为3.
如图,边长为5的正方形ABCD中,CE=DF,若DG2+GE2=29,则CF的长为3.
分析 连接DE,首先证明△DGE是直角三角形,利用勾股定理结合正方形的性质即可求出AE,进一步得出BE.
解答 解:(1)∵四边形ABCD是正方形,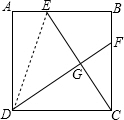
∴DC=BC,∠DCF=∠B=90°,在Rt△DCF和Rt△CBE中,
$\left\{\begin{array}{l}{DF=CE}\\{CD=BC}\end{array}\right.$,
∴△DCF≌△CBE(HL);
∴∠BCE=∠CDF,CF=EB,
∵∠CDF+∠DFC=90°,
∴∠BCE+∠DFC=90°,
∴∠CGF=90°;
∴∠EGD=90°,
∴△DGE是直角三角形,
∵DE2=DG2+GE2=29,
∵AD=5,
∴AE=$\sqrt{D{E}^{2}-A{D}^{2}}$=2,
∴CF=BE=AB-AE=5-2=3.
故答案为3.
点评 此题考查了四边形综合题,涉及到了全等三角形的判定与性质,勾股定理,以及正方形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
7.甲、乙、丙、丁,四名学生在判断钟表的分针和时针互相垂直的时刻时,每人说了两个时刻,说法都对的是( )
| A. | 甲:“3时整和3时30分” | B. | 乙说“6时15分和6时45分” | ||
| C. | 丙说“9时整和12时15分” | D. | 丁说:“3时整和9时整” |
 城市规划期间,欲拆除一电线杆AB,如图,已知大坝背水坡ED的坡角∠EDG=60°,背水坡ED的垂直高度EH为6米,在坝顶E处有一高为1米的测角仪EF,测得杆顶A的仰角为20°,杆底B的俯角为20°,C、D之间是2米宽的人行道,在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封闭?请说明理由(在地面上,以点B为圆心,以AB为半径的圆形区域为危险区域).(tan20°≈0.4,tan70°≈2.7,$\sqrt{3}$≈1.7)
城市规划期间,欲拆除一电线杆AB,如图,已知大坝背水坡ED的坡角∠EDG=60°,背水坡ED的垂直高度EH为6米,在坝顶E处有一高为1米的测角仪EF,测得杆顶A的仰角为20°,杆底B的俯角为20°,C、D之间是2米宽的人行道,在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封闭?请说明理由(在地面上,以点B为圆心,以AB为半径的圆形区域为危险区域).(tan20°≈0.4,tan70°≈2.7,$\sqrt{3}$≈1.7)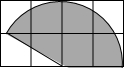 如图所示的格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为$\frac{5}{3}$π;小亮说此圆锥的弧长为$\frac{5}{3}$π,则下列结论正确的是( )
如图所示的格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为$\frac{5}{3}$π;小亮说此圆锥的弧长为$\frac{5}{3}$π,则下列结论正确的是( )