题目内容
4.将分数-$\frac{6}{7}$化为小数是-0.$\stackrel{•}{8}$5714$\stackrel{•}{2}$,则小数点后第2012位上的数是( )| A. | 8 | B. | 5 | C. | 7 | D. | 1 |
分析 分数-$\frac{6}{7}$化为小数是-0.$\stackrel{•}{8}$5714$\stackrel{•}{2}$,循环节是857142,说明此循环小数中这6个数字为一个循环周期,要求小数点后面第2012位上的数字是几,就是求2012里面有几个6,再根据余数确定即可.
解答 解:∵分数-$\frac{6}{7}$化为小数是-0.$\stackrel{•}{8}$5714$\stackrel{•}{2}$,循环节是857142,
∴此循环小数中这6个数字为一个循环周期,
∵2012÷6=335…2;
∴小数点后面第2012位上的数字是5;
故选:B.
点评 此题考查了数字的变化规律,解决此题关键是根据循环节确定6个数字为一个循环周期,进而求出2012里面有几个6,再根据余数确定即可

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.低碳生活是一项符合社会潮流的生活方式.小明的妈妈是低碳生活的响应者.他家现在用70m3水的时间和原来用90m3水的时间相同,已知原来每月比现在每月多用2m3的水.设现在小明家每月用水量为x m3,根据题意下面所列方程中正确的是( )
| A. | $\frac{90}{x+2}$=$\frac{70}{x}$ | B. | $\frac{90}{x-2}$=$\frac{70}{x}$ | C. | $\frac{90}{x}$=$\frac{70}{x+2}$ | D. | $\frac{90}{x}$=$\frac{70}{x-2}$ |
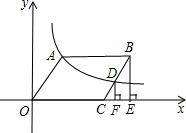 如图,在平面直角坐标系中,?OABC顶点A,B在第一象限,顶点C在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象过点A,交BC于点D,BE⊥x轴于E,DE⊥x轴于F.设△ODF的面积为S1,四边形BEFD的面积为S2,则S1与S2的大小关系为相等.
如图,在平面直角坐标系中,?OABC顶点A,B在第一象限,顶点C在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象过点A,交BC于点D,BE⊥x轴于E,DE⊥x轴于F.设△ODF的面积为S1,四边形BEFD的面积为S2,则S1与S2的大小关系为相等.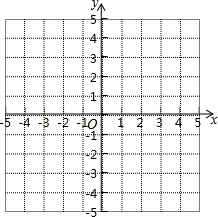 △ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
 如图,矩形ABCD的对角线AC,BD交于点O,若∠DBC=35°,则∠CAB的度数是55°.
如图,矩形ABCD的对角线AC,BD交于点O,若∠DBC=35°,则∠CAB的度数是55°.