题目内容
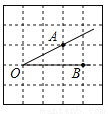
如图，将∠AOB放在边长为1的小正方形组成的网格中，则tan∠AOB= ．
．
【解析】试题分析：过点A作AD⊥OB垂足为D，如图，在直角△ABD中，AD=1，OD=2，则tan∠AOB==．故答案为： ．
练习册系列答案
阅读快车系列答案
相关题目
点P（x，y）关于x轴对称的点P1为______；关于y轴对称的点P2为______；关于原点的对称点P3为______.
（x，-y） （-x，y） （-x，-y）
【解析】点P（x,y）关于x轴对称的点P1为 （x，-y）,关于y轴对称的点P2为 （-x,y）,关于原点的对称点P3为（-x，-y）,故答案为:（x,-y）,（-x,y）,（-x,-y）. 计算：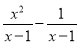 
＝____________.
.x＋1
【解析】试题分析：根据同分母分式相加减，再因式分解后约分即可得： ==x+1.
故答案为：x+1. 如图,图案⑥是由图①~⑤中五种基本图形中的两种拼接而成的,则这两种基本图形是( )
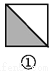
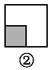
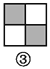
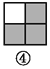
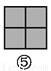
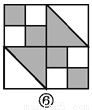
A. ①② B. ①③ C. ①④ D. ③⑤
B
【解析】根据已知图形，利用分割与组合的原理对图形进行分析即可．
【解析】
如图所示：图案⑥是由图①和图③这两种基本图形拼接而成的.
故选：B. 在Rt△ABC中，∠C=90°，CD是斜边AB上的高，如果CD=3，BD=2．求cos∠A的值.
【解析】分析：根据题意画出图形，进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可．
本题解析：
如图所示：
∵∠ACB=90°，∴∠B+∠A=90°，
∵CD⊥AB，∴∠CDA=90°，∴∠B+∠BCD=90°，∴∠BCD=∠A，
∵CD=3，BD=2，∴BC=
∴cosA=cos∠BCD=
故答案为： 在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，下列等式中不一定成立的是（ ）
A. b=atanB B. a=ccosB C. c＝
D. a=bcosA
D
【解析】∵∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，
∴A.tanB= ，则b=atanB，故本选项正确，
B.cosB= ，故本选项正确，
C.sinA= ，故本选项正确，
D.cosA= ，故本选项错误，
故选D． 在Rt△ABC中，∠C=90°，如果AC：BC=3：4，求cosA的值.
【解析】分析:根据题意设AC=3x，BC=4x，故AB=5x，进而利用锐角三角函数关系求出答案．
本题解析：
∵在Rt△ABC中，∠C=90°，AC：BC=3：4，
∴设AC=3x，BC=4x，故AB=5x，
则cosA=
故答案为： 在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，下列等式中不一定成立的是（ ）
A. b=atanB B. a=ccosB C. c＝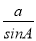
D. a=bcosA
D
【解析】∵∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，
∴A.tanB= ，则b=atanB，故本选项正确，
B.cosB= ，故本选项正确，
C.sinA= ，故本选项正确，
D.cosA= ，故本选项错误，
故选D． 在△ABC中，∠C-90°，若tanB=2，a=1，则b=________．
2
【解析】试题解析：在Rt△ABC中，
∵∠C=90°，
∴AB为斜边．
∴b=AC•tanB
=a•tanB
=2．
故答案为：2.