题目内容
在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式中不一定成立的是( )
A. b=atanB B. a=ccosB C. c=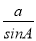 D. a=bcosA
D. a=bcosA
 D
【解析】∵∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,
∴A.tanB= ,则b=atanB,故本选项正确,
B.cosB= ,故本选项正确,
C.sinA= ,故本选项正确,
D.cosA= ,故本选项错误,
故选D.
D
【解析】∵∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,
∴A.tanB= ,则b=atanB,故本选项正确,
B.cosB= ,故本选项正确,
C.sinA= ,故本选项正确,
D.cosA= ,故本选项错误,
故选D.
练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
周长为P的三角形中,最长边m的取值范围是 ( )
A.  B.
B.  C.
C.  D.
D. 
 A
【解析】试题解析:三边相等时,
三边不相等时,最长边
所以,
故选A.
A
【解析】试题解析:三边相等时,
三边不相等时,最长边
所以,
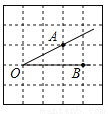
故选A. 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB= .
 .
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: .
.
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: . 比较下列三角函数值的大小:sin40°______cos40°(选填“>”、“=”、“<”)
 【解析】∵cos40°=sin50°,正弦值随着角的增大而增大,
又∵40°<50°,
∴sin40°<cos40°
【解析】∵cos40°=sin50°,正弦值随着角的增大而增大,
又∵40°<50°,
∴sin40°<cos40° sin70°,cos70°,tan70°的大小关系是( )
A. tan70°<cos70°<sin70° B. cos70°<tan70°<sin70°
C. sin70°<cos70°<tan70° D. cos70°<sin70°<tan70°
 D
【解析】根据锐角三角函数的概念,知sin70°<1,cos70°<1,tan70°>1.
又cos70°=sin20°,正弦值随着角的增大而增大,∴sin70°>cos70°=sin20°.
故选D.
D
【解析】根据锐角三角函数的概念,知sin70°<1,cos70°<1,tan70°>1.
又cos70°=sin20°,正弦值随着角的增大而增大,∴sin70°>cos70°=sin20°.
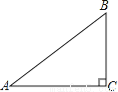
故选D. 如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值为( )
A. 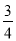 B.
B. 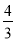 C.
C. 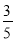 D.
D. 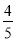
 C
【解析】试题解析:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB=.
cosA=,
故选A.
C
【解析】试题解析:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB=.
cosA=,
故选A. 小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y(米)与时间t(分)的函数图象,则小明回家的速度是每分钟步行 米.
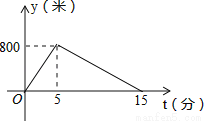
 80
【解析】
试题分析:先分析出小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),再根据路程、时间、速度的关系即可求得.
【解析】
通过读图可知:小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),
所以小明回家的速度是每分钟步行800÷10=80(米).
故答案为:80.
80
【解析】
试题分析:先分析出小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),再根据路程、时间、速度的关系即可求得.
【解析】
通过读图可知:小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),
所以小明回家的速度是每分钟步行800÷10=80(米).
故答案为:80. 根据图中尺规作图的痕迹,先判断得出结论:__________,并说明理由.
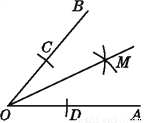
 OM平分∠BOA
【解析】根据全等三角形的判定及性质即可得出结论.
【解析】
如图所示,连接CM,DM,
由作图的痕迹可知,OC=OD,CM=DM.
又因为OM=OM,
所以△COM≌△DOM.
所以∠COM=∠DOM.
所以OM平分∠BOA.
故答案为:OM平分∠BOA.
OM平分∠BOA
【解析】根据全等三角形的判定及性质即可得出结论.
【解析】
如图所示,连接CM,DM,
由作图的痕迹可知,OC=OD,CM=DM.
又因为OM=OM,
所以△COM≌△DOM.
所以∠COM=∠DOM.
所以OM平分∠BOA.
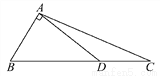
故答案为:OM平分∠BOA. 如图,在直角△BAD中,延长斜边BD到点C,使DC=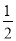 BD,连接AC,若tanB=
BD,连接AC,若tanB=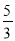 ,则tan∠CAD的值( )
,则tan∠CAD的值( )
A. 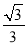 B.
B. 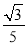 C.
C. 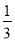 D.
D. 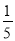
 D
【解析】试题分析:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,即,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴,
∴CE=x,DE= ,
∴AE= ,
∴tan∠CAD=.
故选D.
D
【解析】试题分析:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,即,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴,
∴CE=x,DE= ,
∴AE= ,
∴tan∠CAD=.
故选D. 
