题目内容
计算: 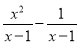 =____________.
=____________.
 .x+1
【解析】试题分析:根据同分母分式相加减,再因式分解后约分即可得: ==x+1.
故答案为:x+1.
.x+1
【解析】试题分析:根据同分母分式相加减,再因式分解后约分即可得: ==x+1.
故答案为:x+1.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
某人先以v1的速度由A地出发去B地,途中在超市购买了一瓶水之后,又以v2的速度继续进行至B地,已知v1<v2 , 下面图象中能表示他从A地到B地的时间t(分钟)与路程s(千米)之间关系的是( )
A. 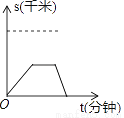 B.
B. 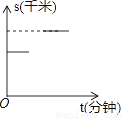
C. 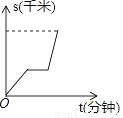 D.
D. 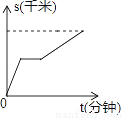
 C
【解析】∵V1<V2,
∴题中图象上表示为开始时图象斜率小,后来斜率大,
又∵途中买了一瓶水,
∴图象有一段平行于x轴,
故选C.
C
【解析】∵V1<V2,
∴题中图象上表示为开始时图象斜率小,后来斜率大,
又∵途中买了一瓶水,
∴图象有一段平行于x轴,
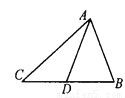
故选C. 如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为11cm,求AC的长.
 8cm.
【解析】试题分析:根据中线的定义知CD=BD,结合三角形的周长公式知AC﹣AB=5cm,又AB+AC=11cm,易求AC的长度.
试题解析:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长﹣△ABD的周长=5cm.
∴AC﹣AB=5cm.
又∵AB+AC=11cm,
∴AC=8cm.即AC的长度是8cm.
8cm.
【解析】试题分析:根据中线的定义知CD=BD,结合三角形的周长公式知AC﹣AB=5cm,又AB+AC=11cm,易求AC的长度.
试题解析:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长﹣△ABD的周长=5cm.
∴AC﹣AB=5cm.
又∵AB+AC=11cm,
∴AC=8cm.即AC的长度是8cm. 周长为P的三角形中,最长边m的取值范围是 ( )
A.  B.
B.  C.
C.  D.
D. 
 A
【解析】试题解析:三边相等时,
三边不相等时,最长边
所以,
故选A.
A
【解析】试题解析:三边相等时,
三边不相等时,最长边
所以,
故选A. 在△ABC中,AB=4a,BC=14,AC=3a.则a的取值范围是 ( )
A. a>2 B. 2<a<14 C. 7<a<14 D. a<14
 B
【解析】试题解析:∵△ABC中,AB=4a,BC=14,AC=3a,
∴解得2
B
【解析】试题解析:∵△ABC中,AB=4a,BC=14,AC=3a,
∴解得2下面是小明化简分式的过程,请仔细阅读,并解答所提出的问题.
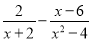
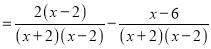 第一步
第一步
=2(x-2)-x+6 第二步
=2x-4-x+6 第三步
=x+2 第四步
小明的解法从第___步开始出现错误,正确的化简结果是______.
 二
【解析】根据分式的加减法,先对分式进行因式分解,然后通分为同分母的分式相加,再化简即可,因此错误在第二步,应为=.
故答案为:二、.
二
【解析】根据分式的加减法,先对分式进行因式分解,然后通分为同分母的分式相加,再化简即可,因此错误在第二步,应为=.
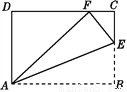
故答案为:二、. 如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24 cm,△ECF的周长为8 cm,求四边形纸片ABCD的周长.
 32(cm)
【解析】根据轴对称的性质可以得到AB=AF,BE=FE,再利用等量代换即可求出四边形纸片ABCD的周长.
解:由题意可知,△ABE和△AFE关于直线AE成轴对称,
所以AB=AF,BE=FE.
因为△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
所以四边形纸片ABCD的周长为:
...
32(cm)
【解析】根据轴对称的性质可以得到AB=AF,BE=FE,再利用等量代换即可求出四边形纸片ABCD的周长.
解:由题意可知,△ABE和△AFE关于直线AE成轴对称,
所以AB=AF,BE=FE.
因为△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
所以四边形纸片ABCD的周长为:
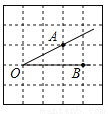
... 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB= .
 .
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: .
.
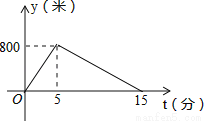
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: . 小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y(米)与时间t(分)的函数图象,则小明回家的速度是每分钟步行 米.
 80
【解析】
试题分析:先分析出小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),再根据路程、时间、速度的关系即可求得.
【解析】
通过读图可知:小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),
所以小明回家的速度是每分钟步行800÷10=80(米).
故答案为:80.
80
【解析】
试题分析:先分析出小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),再根据路程、时间、速度的关系即可求得.
【解析】
通过读图可知:小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),
所以小明回家的速度是每分钟步行800÷10=80(米).
故答案为:80.