题目内容
11.数学兴趣小组活动时,老师带领大家探究《折线中的数学问题》,出示了如图1所示的长方形纸条ABCD,其中AD=BC=3,AB=CD=9,然后在纸条上任意画一条截线段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK.如图2所示:(1)点N到MK的距离是3;
(2)改变折痕MN的位置,△MNK始终什么三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究△MNK的面积S时,发现KN边上的高始终是个不变的值.根据这一发现,他很快研究出△KMN的面积S的最小值为$\frac{9}{2}$,此时∠1的大小可以为45或135°;
(4)小明继续动手操作,发现了△MNK面积S有最大值.请你写出这个最大值为7.5.
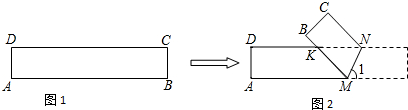
分析 (1)作NE⊥KM于E,NF⊥AB于F,如图所示:则NF=BC=3,由折叠的性质得:∠KMN=∠1,∴NE=NF=3,即点N到MK的距离是3;故答案为:3;
(2)利用翻折变换的性质以及两直线平行内错角相等得出KM=KN;
(3)利用当△KMN的面积最小值为$\frac{9}{2}$时,KN=BC=3,故KN⊥B′M,得出∠1=∠NMB=45°,同理当将纸条向下折叠时,∠1=∠NMB=135°;
(4)分情况讨论:①将矩形纸片对折,使点B与D重合,此时点K也与D重合;②将矩形纸片沿对角线AC对折,此时折痕即为AC两种情况讨论求解.
解答 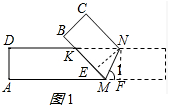 解:(1)作NE⊥KM于E,NF⊥AB于F,如图1所示:
解:(1)作NE⊥KM于E,NF⊥AB于F,如图1所示:
则NF=BC=3,
由折叠的性质得:∠KMN=∠1,
∴NE=NF=3,即点N到MK的距离是3;
故答案为:3;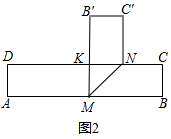
(2)△MNK始终是等腰三角形;理由如下:
∵长方形ABCD中,AB∥CD,
∴∠1=∠MNK,
∵∠1=∠KMN,
∴∠MNK=∠KMN,
∴KM=KN;即△MNK是等腰三角形;
(3)如图2,当△KMN的面积最小值为$\frac{9}{2}$时,KN=BC=3,故KN⊥B′M,
∵∠NMB=∠KMN,∠KMB=90°,
∴∠1=∠NMB=45°,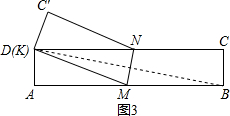
同理当将纸条向下折叠时,∠1=∠NMB=135°
故答案为:45或135;
(4)分两种情况:
①如图3,将矩形纸片对折,使点B与D重合,此时点K也与D重合.
MK=MB=x,则AM=9-x.
由勾股定理得::32+(9-x)2=x2,
解得x=5.
∴MD=ND=5.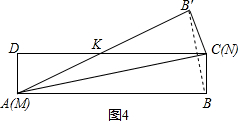
S△MNK=S△MND=$\frac{1}{2}$×3×5=7.5.
②如图4,将矩形纸片沿对角线AC对折,此时折痕即为AC.
MK=AK=CK=x,则DK=9-x.
同理可得MK=NK=5.
∵MD=3,
∴S△MNK=$\frac{1}{2}$×3×5=7.5.
△MNK的面积最大值为7.5;
故答案为:7.5.
点评 本题是四边形综合题目,考查了翻折变换(折叠问题),矩形的性质,勾股定理,三角形的面积计算,注意分类思想的运用,本题综合性较强,有一定的难度.

 习题精选系列答案
习题精选系列答案| A. | 1 | B. | 4 | C. | 1或4 | D. | 不确定 |
| A. | 2+10x≥87 | B. | 2+10x≤87 | C. | 10+8x≤87 | D. | 10+8x≥87 |
| A. | x8-x4=x4 | B. | (a4)2=a16 | C. | (a3b2)3=a4b5 | D. | a6÷a2=a4 |
 甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法错误的是( )
甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法错误的是( )| A. | 甲车的速度为50km/h | B. | 乙车用了2h到达B城 | ||
| C. | 甲车出发4h时,乙车追上甲车 | D. | 两车共有2次相距50km |
| A. | $\left\{\begin{array}{l}2x-2y=18\\ 5x+4y=18\end{array}\right.$ | B. | $\left\{\begin{array}{l}2x+2y=18\\ 5x-4y=18\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}2x+2y=18\\ 4y-5x=18\end{array}\right.$ | D. | $\left\{\begin{array}{l}2x+2y=18\\ 5x+4y=18\end{array}\right.$ |
 如图所示,在四边形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
如图所示,在四边形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).