题目内容
3.我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”,这个三角形给出了(a+b)n(n=1,2,34…)的展开式的系数规律(按a的次数由大到小的顺序);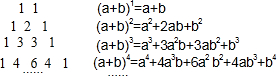
请依据上述规律,写出${(x-\frac{2}{x})}^{2017}$展开式中含x2015项的系数是-4034.
分析 首先确定x2015是展开式中第几项,根据杨辉三角即可解决问题.
解答 解:(x-$\frac{2}{x}$)2017展开式中含x2015项的系数,
由(x-$\frac{2}{x}$)2017=x2017-2017•x2016•($\frac{2}{x}$)+…
可知,展开式中第二项为-2017•x2016•($\frac{2}{x}$)=-4034x2015,
∴(x-$\frac{2}{x}$)2017展开式中含x2015项的系数是-4034,
故答案为:-4034.
点评 本题考查整式的混合运算、杨辉三角等知识,解题的关键是灵活运用杨辉三角解决问题,属于中考常考题型.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
13.已知a2-5a-1=0,则a2+$\frac{1}{{a}^{2}}$的值为( )
| A. | 5 | B. | 25 | C. | 23 | D. | 27 |
18.下列各式计算正确的是( )
| A. | ${(-\frac{1}{2}{ab}^{2})}^{2}$=$\frac{1}{4}$ab4 | B. | (-1+b)(-b-1)=1-b2 | C. | 5xy2-xy2=4 | D. | (a-b)2=a2+b2 |
8. 如图,把半径为0.5的圆放到数轴上,圆上一点A与表示1的点重合,圆沿着数轴正方向滚动一周,此时点A表示的数是( )
如图,把半径为0.5的圆放到数轴上,圆上一点A与表示1的点重合,圆沿着数轴正方向滚动一周,此时点A表示的数是( )
 如图,把半径为0.5的圆放到数轴上,圆上一点A与表示1的点重合,圆沿着数轴正方向滚动一周,此时点A表示的数是( )
如图,把半径为0.5的圆放到数轴上,圆上一点A与表示1的点重合,圆沿着数轴正方向滚动一周,此时点A表示的数是( )| A. | π | B. | π+1 | C. | 2π | D. | π-1 |
 如图,AB是⊙O的直径,点P在⊙O上,且PA=PB,点M是⊙O外一点,MB与⊙O相切于点B,连接OM,过点A作AC∥OM交⊙O于点C,连接BC交OM于点D.
如图,AB是⊙O的直径,点P在⊙O上,且PA=PB,点M是⊙O外一点,MB与⊙O相切于点B,连接OM,过点A作AC∥OM交⊙O于点C,连接BC交OM于点D. 如图,已知∠1和∠2互余,∠2与∠3互补,∠3=140°,求∠4的度数.
如图,已知∠1和∠2互余,∠2与∠3互补,∠3=140°,求∠4的度数. 如图,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{k_2}{x}$的图象相交与A,B两点,其横坐标分别为2和6,则不等式k1x<$\frac{k_2}{x}$-b的解集是0<x<2或x>6.
如图,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{k_2}{x}$的图象相交与A,B两点,其横坐标分别为2和6,则不等式k1x<$\frac{k_2}{x}$-b的解集是0<x<2或x>6.