Question

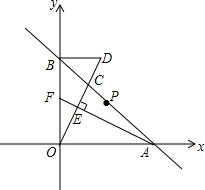如图，直线y=-x+2与x轴、y轴分别交于点A、B两点，点C在线段AB上（不含端点A、B）．
（1）求A、B两点的坐标；
（2）若BD∥OA交直线OC于D，AE⊥OC，垂足为E，交OB于F，P为AB中点．当点C在线段BP上运动时，求证：BD+BF的值不变．

Answer 1

考点：一次函数综合题

专题：

分析：（1）在直线y=-x+2中分别令y=0、x=0，可求得A、B两点的坐标；
（2）根据条件可证得△BDO≌△FOA，可得到BD=FO，从而可得到BD+BF=BO，可得出结论．

解答：（1）解：在直线y=-x+2中，令y=0可得x=2，令x=0可得y=2，
∴A（2，0）B（0，2）；
（2）证明：∵BD∥OA，AE⊥OC，
∴∠D=∠DOA，
∵∠DOA+∠DOF=90°，∠AFO+∠DOF=90°，
∴∠DOA=∠AFO，
∴∠D=∠AFO，
在△DBO和△FOA中，

∠D=∠AFO ∠DBO=∠AOF OB=OA

，
∴△DBO≌△FOA（AAS），
∴BD=FO，
∴BD+BF=FO+BF=BO，
∵BO=2，
∴BD+BF=2，
即BD+BF是定值不变．

点评：本题主要考查直线与坐标轴的交点及全等三角形的判定和性质，求直线与两坐标轴的交点可以分别令y=0和x=0得到，在（2）中把BD、BF通过证明三角形全等转移到一条线段BO上是解题的关键．本题难度不大，注重了基础知识的考查，容易得分．