题目内容
 如图,D、E是Rt△ABC的边AB、BC的中点,M、N在斜边AC上,且AM=MN=CN,DM、EN的延长线交于点P.求证:
如图,D、E是Rt△ABC的边AB、BC的中点,M、N在斜边AC上,且AM=MN=CN,DM、EN的延长线交于点P.求证:(1)四边形BNPM是平行四边形;
(2)四边形ABCP是矩形.
考点:矩形的判定,平行四边形的判定
专题:证明题
分析:(1)利用中位线的性质定理得到DM∥BN、NE∥BM,利用两组对边平行且相等的四边形是平行四边形进行判定即可;
(2)首先判定四边形ABCP是平行四边形,然后利用有一个角是直角的平行四边形是矩形进行判定.
(2)首先判定四边形ABCP是平行四边形,然后利用有一个角是直角的平行四边形是矩形进行判定.
解答: 证明:(1)连接BP,交AC于点O.
证明:(1)连接BP,交AC于点O.
∵AD=BD,AM=MN,
∴DM是△ABN的中位线,
∴DM∥BN,同理NE∥BM,
∴四边形BNPM是平行四边形;
(2)∵四边形BNPM是平行四边形,
∴BO=PO,MO=NO,
∵AM=CN,
∴OA=OC,
∴四边形ABCP是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形.
 证明:(1)连接BP,交AC于点O.
证明:(1)连接BP,交AC于点O.∵AD=BD,AM=MN,
∴DM是△ABN的中位线,
∴DM∥BN,同理NE∥BM,
∴四边形BNPM是平行四边形;
(2)∵四边形BNPM是平行四边形,
∴BO=PO,MO=NO,
∵AM=CN,
∴OA=OC,
∴四边形ABCP是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形.
点评:本题考查了平行四边形的判定、矩形的判定及性质等知识,解题的关键是熟练掌握平行四边形、矩形的判定定理,难度不大.

练习册系列答案
相关题目
 根据如图所示的流程图中的程序,当输入数值x为-4时,输出数值y为( )
根据如图所示的流程图中的程序,当输入数值x为-4时,输出数值y为( )| A、6 | B、7 | C、8 | D、9 |
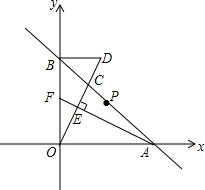 如图,直线y=-x+2与x轴、y轴分别交于点A、B两点,点C在线段AB上(不含端点A、B).
如图,直线y=-x+2与x轴、y轴分别交于点A、B两点,点C在线段AB上(不含端点A、B). 一艘轮船沿自西向东航行,在A处测得某岛C的北偏东60°的方向上,船前进8海里后到达B处,再测得C岛在北偏东30°方向上,问船再前进多少海里与C岛最近?最近距离是多少?
一艘轮船沿自西向东航行,在A处测得某岛C的北偏东60°的方向上,船前进8海里后到达B处,再测得C岛在北偏东30°方向上,问船再前进多少海里与C岛最近?最近距离是多少? 由6个相同的小立方块搭成的几何体如图所示,请画出从三个方向看所得到的形状图.
由6个相同的小立方块搭成的几何体如图所示,请画出从三个方向看所得到的形状图. 如图所示,∠BAC=∠CAE=∠EAD,试问△ABC中哪个角最大?哪个角最小?说明你的理由.
如图所示,∠BAC=∠CAE=∠EAD,试问△ABC中哪个角最大?哪个角最小?说明你的理由.