题目内容
 如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=
如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=| k |
| x |
①双曲线的解析式为y=
| 20 |
| x |
| 4 |
| 3 |
| 5 |
其中正确的结论有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:反比例函数综合题,完全平方公式,待定系数法求反比例函数解析式,勾股定理,菱形的性质,锐角三角函数的定义
专题:
分析:过点C作CH⊥OA于H,运用菱形的面积公式可求出CH,然后根据勾股定理求出OH,从而可求出点C的坐标及tan∠COA的值;然后根据中点坐标公式可求出点D的坐标,运用待定系数法可求出双曲线的解析式;由yE=yC就可求出点E的坐标;根据勾股定理可求出AC2+OB2,然后运用完全平方公式就可求出AC+OB的值.
解答:解:过点C作CH⊥OA于H,如图所示.
∵A点的坐标为(10,0),
∴OA=10.
∵四边形OABC是菱形,
∴OC=OA=10,S菱形OABC=
OB•AC=OA•CH.
∵OB•AC=160,OA=10,
∴CH=8,
∴OH=
=
=6,
∴点C的坐标为(6,8),tan∠COA=
=
=
.
∵点C的坐标为(6,8),A点的坐标为(10,0),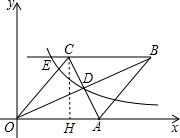
∴线段AC的中点D的坐标为(
,
)即(8,4).
∵双曲线y=
(x>0)经过D点,
∴k=8×4=32,
∴双曲线的解析式为y=
(x>0).
∵点E在双曲线y=
(x>0)上,且yE=yC=8,
∴xE=4,即点E的坐标为(4,8).
∵四边形OABC是菱形,
∴OB⊥AC,OB=2OD,AC=2AD,
∴OB2+AC2=4OD2+4AD2=4OA2=400,
∴(AC+OB)2=AC2+OB2+2AC•OB=400+320=720,
∴AC+OB=
=12
.
综上所述:正确的有②、③、④,共3个.
故选:D.
∵A点的坐标为(10,0),
∴OA=10.
∵四边形OABC是菱形,
∴OC=OA=10,S菱形OABC=
| 1 |
| 2 |
∵OB•AC=160,OA=10,
∴CH=8,
∴OH=
| OC2-CH2 |
| 102-82 |
∴点C的坐标为(6,8),tan∠COA=
| CH |
| OH |
| 8 |
| 6 |
| 4 |
| 3 |
∵点C的坐标为(6,8),A点的坐标为(10,0),

∴线段AC的中点D的坐标为(
| 6+10 |
| 2 |
| 8+0 |
| 2 |
∵双曲线y=
| k |
| x |
∴k=8×4=32,
∴双曲线的解析式为y=
| 32 |
| x |
∵点E在双曲线y=
| 32 |
| x |
∴xE=4,即点E的坐标为(4,8).
∵四边形OABC是菱形,
∴OB⊥AC,OB=2OD,AC=2AD,
∴OB2+AC2=4OD2+4AD2=4OA2=400,
∴(AC+OB)2=AC2+OB2+2AC•OB=400+320=720,
∴AC+OB=
| 720 |
| 5 |
综上所述:正确的有②、③、④,共3个.
故选:D.
点评:本题主要考查了菱形的性质、用待定系数法求双曲线的解析式、勾股定理、三角函数、中点坐标公式、完全平方公式等知识,解决本题的关键是根据菱形的面积公式求出OA边上的高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
以
为解的二元一次方程组( )
|
| A、有且只有1个 |
| B、有且只有2个 |
| C、有且只有3个 |
| D、有无数个 |
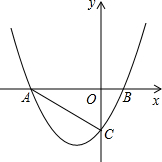 已知:二次函数y=
已知:二次函数y=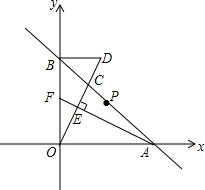 如图,直线y=-x+2与x轴、y轴分别交于点A、B两点,点C在线段AB上(不含端点A、B).
如图,直线y=-x+2与x轴、y轴分别交于点A、B两点,点C在线段AB上(不含端点A、B). 由6个相同的小立方块搭成的几何体如图所示,请画出从三个方向看所得到的形状图.
由6个相同的小立方块搭成的几何体如图所示,请画出从三个方向看所得到的形状图.