题目内容
设ax4+bx3+cx2+dx+e=(x-2)4,求代数式的值:
(1)a+b+c+d+e;
(2)a+c.
(1)a+b+c+d+e;
(2)a+c.
考点:代数式求值
专题:计算题
分析:(1)把x=1代入已知等式求出a+b+c+d+e的值即可;
(2)把x=-1代入已知等式求出a-b+c-d+e的值,与(1)结果两边相加求出a+c+e的值,即可确定出a+c的值.
(2)把x=-1代入已知等式求出a-b+c-d+e的值,与(1)结果两边相加求出a+c+e的值,即可确定出a+c的值.
解答:解:(1)把x=1代入得:a+b+c+d+e=1①;
(2)把x=-1代入得:a-b+c-d+e=81②,
把x=0代入得:e=16,
①+②得:2(a+c+e)=82,即a+c+e=41,
则a+c=41-16=25.
(2)把x=-1代入得:a-b+c-d+e=81②,
把x=0代入得:e=16,
①+②得:2(a+c+e)=82,即a+c+e=41,
则a+c=41-16=25.
点评:此题考查了代数式求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
下列说法中正确的是( )
| A、61550 保留两个有效数字为6.1×104 |
| B、近似数2.30×10-1有3个有效数字,精确到了百分位 |
| C、近似数15.04万有4个有效数字,精确到了百位 |
| D、4.6502精确到0.001为4.65,有3个有效数字 |
 根据如图所示的流程图中的程序,当输入数值x为-4时,输出数值y为( )
根据如图所示的流程图中的程序,当输入数值x为-4时,输出数值y为( )| A、6 | B、7 | C、8 | D、9 |
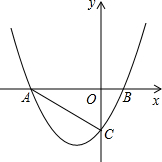 已知:二次函数y=
已知:二次函数y=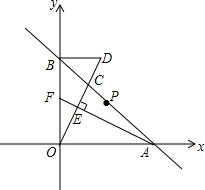 如图,直线y=-x+2与x轴、y轴分别交于点A、B两点,点C在线段AB上(不含端点A、B).
如图,直线y=-x+2与x轴、y轴分别交于点A、B两点,点C在线段AB上(不含端点A、B). 如图所示,∠BAC=∠CAE=∠EAD,试问△ABC中哪个角最大?哪个角最小?说明你的理由.
如图所示,∠BAC=∠CAE=∠EAD,试问△ABC中哪个角最大?哪个角最小?说明你的理由.