题目内容

18．在△EFG中，∠G=90°，EG=6，EF=10，tanE=（　　）
A．$\frac{3}{4}$B．$\frac{4}{3}$C．$\frac{3}{5}$D．$\frac{5}{3}$

分析 根据勾股定理得出FG，再利用三角函数的定义即可得出答案．

解答 解：∵∠G=90°，EG=6，EF=10，
∴FG=8，
∴tanE=$\frac{FG}{EG}$=$\frac{8}{6}$=$\frac{4}{3}$．
故选B．

点评 本题考查了锐角三角函数的定义，掌握三角函数的计算公式是解题的关键．

练习册系列答案
相关题目
8．二次函数y=-x2-2x+7的图象的对称轴是（　　）
A．直线x=2B．直线x=-2C．直线x=1D．直线x=-1
9．解分式方程：
（1）$\frac{1}{2x}=\frac{2}{x+3}$
（2）$\frac{x+1}{x-1}-\frac{4}{{{x^2}-1}}=1$．
6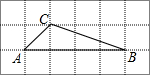．如图，A，B，C三点在正方形网络线的交点处，则tanB的值为（　　）
A．$\frac{1}{3}$B．3C．$\frac{{\sqrt{10}}}{3}$D．$\frac{{\sqrt{10}}}{10}$
13．如图，已知这是一座圆弧形涵洞的入口的示意图，涵洞的最高点C到地面AB的距离为6米，涵洞入口地面的宽度AB为4米，请你求这座涵洞圆弧所在圆的半径长．
3．估计$\sqrt{5}$-1的值在哪两个整数之间（　　）
A．1与2B．2与3C．3与4D．4与5
10．若二次函数y=x2+2m-1的图象经过原点，则m的值是$\frac{1}{2}$．
7．将同样大小的正方形按下列规律摆放，重叠部分涂上阴影，则下面图案中，第1个图案有3个正方形，第2个图案有7个正方形，那么：

（1）第六个图案中有23个正方形；
（2）若第n个图案中有7999个正方形，则n=2000．
8．化简：
（1）x（2x-1）-（x-3）2
（2）（$\frac{4x+4}{x+2}$-x-2）÷$\frac{{x}^{2}-2x}{{x}^{2}-4}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网