题目内容
13．
如图，已知这是一座圆弧形涵洞的入口的示意图，涵洞的最高点C到地面AB的距离为6米，涵洞入口地面的宽度AB为4米，请你求这座涵洞圆弧所在圆的半径长．
分析 连接OA，构造直角三角形．根据垂径定理和勾股定理进行计算得出答案即可．
解答 
解：依题意，CD过点O且垂直于AB，连接OA，
设半径为x米，
所以AD=DB=2，
在Rt△ADO中，由勾投定理，有OA2=OD2+AD2，
即x2=（6-x）2+22，
得x=$\frac{10}{3}$．
答：这座涵洞圆弧所在圆的半径为$\frac{10}{3}$米．
点评 本题考查的是垂径定理的应用及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
如图，正方形ABCD和正方形EFGH的对角线BD、FH都在x轴上，O、M分别为正方形ABCD和正方形EFGH的中心（正方形对角线的交点称为正方形的中心），O为平面直角坐标系的原点，OD=3，MH=2，DF=3．
4．有一批水果，包装质量为每筐25千克，现抽取10筐样品进行检测，结果称重如下（单位：千克）：21，24，27，28，25，26，22，23，25，26．为了求得10筐样品的总质量，我们可以选取一个恰当的基准数进行简化运算．
（1）你认为选取的一个恰当的基准数为25千克；
（2）根据你选取的基准数，用正、负数填写上表；
（3）这10筐水果的总质量是多少千克？
| 原质量 | 21 | 24 | 27 | 28 | 25 | 26 | 22 | 23 | 25 | 26 |
| 与基准数的差距 |
（2）根据你选取的基准数，用正、负数填写上表；
（3）这10筐水果的总质量是多少千克？
8．
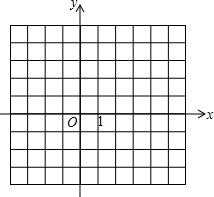在二次函数y=ax2+bx+c（a≠0）中，函数y与自变量x的部分对应值如表：
（1）求这个二次函数的解析式及m的值；
（2）在平面直角坐标系中，用描点法画出这个二次函数的图象（不用列表）；
（3）当y＜3时，则x的取值范围是0＜x＜4．
在二次函数y=ax2+bx+c（a≠0）中，函数y与自变量x的部分对应值如表：| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | m | … |
（2）在平面直角坐标系中，用描点法画出这个二次函数的图象（不用列表）；
（3）当y＜3时，则x的取值范围是0＜x＜4．
18．在△EFG中，∠G=90°，EG=6，EF=10，tanE=（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{5}{3}$ |
2．方程4x=-8的解是（ ）
| A． | x=-2 | B． | x=-$\frac{1}{2}$ | C． | x=$\frac{1}{2}$ | D． | x=2 |