题目内容
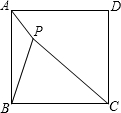 如图,P是正方形ABCD内一点,PA=3,PB=6,PC=9.求∠APB的度数.
如图,P是正方形ABCD内一点,PA=3,PB=6,PC=9.求∠APB的度数.考点:旋转的性质,勾股定理的逆定理,正方形的性质
专题:计算题
分析:先根据正方形的性质得到BA=BC,∠ABC=90°,于是把△APB绕点B顺时针旋转90°得到△CBE,连结PE,如图,再根据旋转的性质得BE=BP=6,CE=AP=3,∠CEB=∠APB,∠PBE=90°,所以△PBE为等腰直角三角形,则PE=
PB=6
,∠PEB=45°,然后利用勾股定理的逆定理可证明△PEC为直角三角形,得到∠PEC=90°,则∠CEB=∠PEC+∠PEB=135°,因此∠APB=135°.
| 2 |
| 2 |
解答: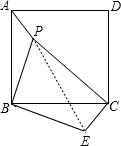 解:∵四边形ABCD为正方形,
解:∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
∴把△APB绕点B顺时针旋转90°得到△CBE,连结PE,如图,
∴BE=BP=6,CE=AP=3,∠CEB=∠APB,∠PBE=90°,
∴△PBE为等腰直角三角形,
∴PE=
PB=6
,∠PEB=45°
在△PCE中,∵PC2=81,CE2=9,PE2=72,
∴PC2=CE2+PE2,
∴△PEC为直角三角形,∠PEC=90°,
∴∠CEB=∠PEC+∠PEB=135°,
∴∠APB=135°.
 解:∵四边形ABCD为正方形,
解:∵四边形ABCD为正方形,∴BA=BC,∠ABC=90°,
∴把△APB绕点B顺时针旋转90°得到△CBE,连结PE,如图,
∴BE=BP=6,CE=AP=3,∠CEB=∠APB,∠PBE=90°,
∴△PBE为等腰直角三角形,
∴PE=
| 2 |
| 2 |
在△PCE中,∵PC2=81,CE2=9,PE2=72,
∴PC2=CE2+PE2,
∴△PEC为直角三角形,∠PEC=90°,
∴∠CEB=∠PEC+∠PEB=135°,
∴∠APB=135°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质和勾股定理的逆定理.

练习册系列答案
相关题目
调查下列问题,适合全面调查的是( )
| A、检测某城市的空气质量 |
| B、估计某池塘中现有鱼的数量 |
| C、某单位招聘员工,对应聘人员进行面试 |
| D、调查某种节能灯的使用寿命 |
下列计算正确的是( )
| A、2a+3b=5ab |
| B、5y2-3y2=3 |
| C、-p2-p2=-2p2 |
| D、7mn-7=mn |
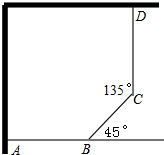 用30m长的篱笆和相邻两面墙围成如图形状的小花园,其中AB=CD.设BC=x(m),小花园的面积为S(m2).求:
用30m长的篱笆和相邻两面墙围成如图形状的小花园,其中AB=CD.设BC=x(m),小花园的面积为S(m2).求: