题目内容
在平面直角坐标系中,矩形OABC的顶点A、C分别在x、y轴的正半轴上.反比例函数y=
的图象分别交边AB、BC于D、E,交对角线OB于F.
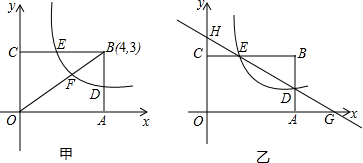
(1)如图甲,顶点B的坐标为(4,3),若点F是OB的中点,则k= ,
= .
(2)如图乙,点B的坐标为(m,n),
①试探寻线段BD与BE的长度关系,并说明理由;
②设直线DE分别与x轴、y轴交与点G、H,试探寻线段DG与EH的长度关系,并说明理由.
| k |
| x |
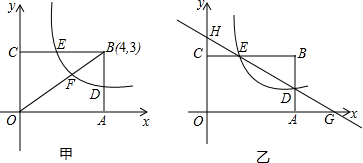
(1)如图甲,顶点B的坐标为(4,3),若点F是OB的中点,则k=
| BD |
| BE |
(2)如图乙,点B的坐标为(m,n),
①试探寻线段BD与BE的长度关系,并说明理由;
②设直线DE分别与x轴、y轴交与点G、H,试探寻线段DG与EH的长度关系,并说明理由.
考点:反比例函数综合题
专题:
分析:(1)根据顶点B的坐标和点F是OB的中点,得出点F的坐标,再根据点F在反比例函数y=
的图象上,求出反比例函数的解析式,从而求出BD、BE的长,再代入计算即可得出答案.
(2)①根据点B的坐标为(m,n),表示出点D的坐标和点E的坐标,从而得出AD=
,EC=
,再根据BD=AB-AD和BE=BC-CE,求出
,即可得出答案;
②根据
=
=
和
=
=
,即可得出DG=HE.
| k |
| x |
(2)①根据点B的坐标为(m,n),表示出点D的坐标和点E的坐标,从而得出AD=
| k |
| m |
| k |
| n |
| BD |
| BE |
②根据
| DG |
| DE |
| AD |
| BD |
| k |
| mn-k |
| HE |
| DE |
| CE |
| DE |
| k |
| mn-k |
解答:解:(1)∵顶点B的坐标为(4,3),点F是OB的中点,
∴点F的坐标为:(2,
),
∵点F在反比例函数y=
的图象上,
∴k=xy=2×
=3,
∴当x=4时,y=
,
即AD=
,
∴BD=AB-AD=3-
=
,
当y=3时,x=
=2,
∴CE=2,
∴BE=BC-CE=4-2=2,
∴
=
;
故答案为:3;
;
(2)①∵点B的坐标为(m,n),
∴点D的坐标是(m,
),点E的坐标是(
,n),
∴AD=
,EC=
,
∴BD=AB-AD=n-
,BE=BC-CE=m-
,
∴
=
=
,
②∵
=
=
=
,
=
=
=
,
∴
=
,
∴DG=HE.
∴点F的坐标为:(2,
| 3 |
| 2 |
∵点F在反比例函数y=
| k |
| x |
∴k=xy=2×
| 3 |
| 2 |
∴当x=4时,y=
| 3 |
| 4 |
即AD=
| 3 |
| 4 |
∴BD=AB-AD=3-
| 3 |
| 4 |
| 9 |
| 4 |
当y=3时,x=
| 3 | ||
|
∴CE=2,
∴BE=BC-CE=4-2=2,
∴
| BD |
| BE |
| 9 |
| 8 |
故答案为:3;
| 9 |
| 8 |
(2)①∵点B的坐标为(m,n),
∴点D的坐标是(m,
| k |
| m |
| k |
| n |
∴AD=
| k |
| m |
| k |
| n |
∴BD=AB-AD=n-
| k |
| m |
| k |
| n |
∴
| BD |
| BE |
n-
| ||
m-
|
| mn2-nk |
| m2n-mk |
②∵
| DG |
| DE |
| AD |
| BD |
| ||
n-
|
| k |
| mn-k |
| HE |
| DE |
| CE |
| DE |
| ||
m-
|
| k |
| mn-k |
∴
| DG |
| DE |
| HE |
| DE |
∴DG=HE.
点评:此题考查了反比例函数的综合,用到的知识点是反比例函数的图象与性质、相似三角形的判定与性质、矩形的性质,关键是用m、n、k表示出线段的长度.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
点A(x1,y1)和B(x2,y2)都在直线y=-x上,且x1>x2,则y1与y2的关系是( )
| A、y1≥y2 |
| B、y1=y2 |
| C、y1<y2 |
| D、y1>y2 |
约分
的结果是( )
| 2xy |
| -x2y |
| A、-1 | ||
| B、-2x | ||
C、-
| ||
D、
|
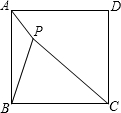 如图,P是正方形ABCD内一点,PA=3,PB=6,PC=9.求∠APB的度数.
如图,P是正方形ABCD内一点,PA=3,PB=6,PC=9.求∠APB的度数. 如图,AB=AE,AC=AD,BD=CE,求证:△ABC≌△ADE.
如图,AB=AE,AC=AD,BD=CE,求证:△ABC≌△ADE.