题目内容
盐徐高速公路养护小组,乘车沿东西向公路巡视维护,如果约定向东为正,向西为负,当天的行驶记录如下(单位:千米):-9,+17,+3,-15,+13,-3,
(1)养护小组共走了多远?
(2)若汽车耗油量为0.4L/km,则这次养护共耗油多少升?
(1)养护小组共走了多远?
(2)若汽车耗油量为0.4L/km,则这次养护共耗油多少升?
考点:正数和负数
专题:
分析:(1)将每次记录的绝对值相加即可;
(2)(1)中得到的值×0.4升就是这次养护共耗油多少升.
(2)(1)中得到的值×0.4升就是这次养护共耗油多少升.
解答:解:(1)9+17+3+15+13+3=60(千米);
答:养护小组共走了60千米;
(2)60×0.4=24(L),
答:这次养护共耗油24升.
答:养护小组共走了60千米;
(2)60×0.4=24(L),
答:这次养护共耗油24升.
点评:此题考查的知识点是正数和负数,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.

练习册系列答案
相关题目
若
(y+1)与3-2y互为相反数,则y等于( )
| 1 |
| 3 |
| A、-2 | ||
| B、2 | ||
C、
| ||
D、-
|
若α,β是方程x2+(k-2)x-k+2=0的两个相异的实根,且0<α-β<2
,那么k的取值范围是( )
| 2 |
A、-2
| ||||
B、2<k<2
| ||||
| C、-2<k<2 | ||||
D、-2
|
若将抛物线y=-x2+2x-2先向右平移一个单位,再沿x轴翻折到第一象限,然后向右平移一个单位,再沿y轴翻折到第二象限,…,以此类推,如果把向右平移一个单位,再沿一条坐标轴翻折一次记作1次变换,那么拋物线y=-x2-2x-2经过第50次变换后,所得抛物线的函数解析式为( )
| A、y=(x+3)2+1 |
| B、y=(x-2)2+1 |
| C、y=-(x+2)2-1 |
| D、y=-(x+3)2+1 |
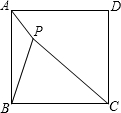 如图,P是正方形ABCD内一点,PA=3,PB=6,PC=9.求∠APB的度数.
如图,P是正方形ABCD内一点,PA=3,PB=6,PC=9.求∠APB的度数.