题目内容
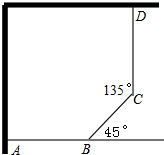 用30m长的篱笆和相邻两面墙围成如图形状的小花园,其中AB=CD.设BC=x(m),小花园的面积为S(m2).求:
用30m长的篱笆和相邻两面墙围成如图形状的小花园,其中AB=CD.设BC=x(m),小花园的面积为S(m2).求:(1)S关于x的函数表达式;
(2)S的最大值,以及当S达到最大值时AB,BC,CD的长.
考点:二次函数的应用
专题:应用题
分析:(1)延长DC交AB于E点,如图,先证明△BCE为等腰直角三角形,则BE=CE=
x,由于AB=DC=
=15-
x,则AE=DE=AB+BE=15-
x+
x,然后利用小花园的面积等于正方形的面积减去等腰直角三角形的面积得到S=(15-
x+
x)2-
•(
x)2=-
x2+15(
-1)x+225;
(2)把(1)的解析式进行配方得到S=-
(x-15)2+
,则根据二次函数的最值问题得到当x=15时,S有大值为
,然后计算15-
x得到AB和CD的长.
| ||
| 2 |
| 30-x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
(2)把(1)的解析式进行配方得到S=-
| ||
| 2 |
225(
| ||
| 2 |
225
| ||
| 2 |
| 1 |
| 2 |
解答: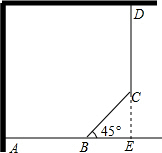 解:(1)延长DC交AB于E点,如图,
解:(1)延长DC交AB于E点,如图,
∵∠DCB=135°,
∴∠BCE=45°
而∠CBE=45°,
∴△BCE为等腰直角三角形,
∴BE=CE=
x,
∵AB=DC=
=15-
x,
∴AE=DE=AB+BE=15-
x+
x,
∴S=(15-
x+
x)2-
•(
x)2
=-
x2+15(
-1)x+225
(2)S=-
(x-15)2+
,
∵a=-
<0,
∴当x=15时,S有大值为
,
此时BC=15cm,AB=DC=15-
x=7.5(cm).
 解:(1)延长DC交AB于E点,如图,
解:(1)延长DC交AB于E点,如图,∵∠DCB=135°,
∴∠BCE=45°
而∠CBE=45°,
∴△BCE为等腰直角三角形,
∴BE=CE=
| ||
| 2 |
∵AB=DC=
| 30-x |
| 2 |
| 1 |
| 2 |
∴AE=DE=AB+BE=15-
| 1 |
| 2 |
| ||
| 2 |
∴S=(15-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=-
| ||
| 2 |
| 2 |
(2)S=-
| ||
| 2 |
225(
| ||
| 2 |
∵a=-
| ||
| 2 |
∴当x=15时,S有大值为
225
| ||
| 2 |
此时BC=15cm,AB=DC=15-
| 1 |
| 2 |
点评:本题考查了二次函数的应用:几何图形中的最值问题,几何图形中的二次函数问题常见的有:几何图形中面积的最值,用料的最佳方案以及动态几何中的最值的讨论.

练习册系列答案
相关题目
一元二次不等式ax2+bx+2>0的解为-
<x<
,则a-b=( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、10 | B、-14 |
| C、-10 | D、-8 |
计算
-
的结果是( )
| 2 |
| a-2 |
| a |
| a-2 |
| A、1 | B、-1 | C、2 | D、-2 |
约分
的结果是( )
| 2xy |
| -x2y |
| A、-1 | ||
| B、-2x | ||
C、-
| ||
D、
|
若将抛物线y=-x2+2x-2先向右平移一个单位,再沿x轴翻折到第一象限,然后向右平移一个单位,再沿y轴翻折到第二象限,…,以此类推,如果把向右平移一个单位,再沿一条坐标轴翻折一次记作1次变换,那么拋物线y=-x2-2x-2经过第50次变换后,所得抛物线的函数解析式为( )
| A、y=(x+3)2+1 |
| B、y=(x-2)2+1 |
| C、y=-(x+2)2-1 |
| D、y=-(x+3)2+1 |
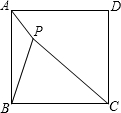 如图,P是正方形ABCD内一点,PA=3,PB=6,PC=9.求∠APB的度数.
如图,P是正方形ABCD内一点,PA=3,PB=6,PC=9.求∠APB的度数.