题目内容
若直线y=2x-1与二次函数y=-x2+3x+5的图象交于A、B两点,求以A、B及原点O为顶点的三角形的面积.
考点:二次函数的性质
专题:
分析:联立两函数解析式求解即可得到点A、B的坐标;求出直线与y轴的交点,再根据三角形的面积公式列式计算即可得解.
解答:解:联立
,
解得
,
,
所以,点A、B的坐标分别为(-2,-5),(3,5),
令x=0,则y=-1,
所以,直线与y轴的交点坐标为(0,-1),
所以,以A、B及原点O为顶点的三角形的面积=
×1×(2+3)=
.
|
解得
|
|
所以,点A、B的坐标分别为(-2,-5),(3,5),
令x=0,则y=-1,
所以,直线与y轴的交点坐标为(0,-1),
所以,以A、B及原点O为顶点的三角形的面积=
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查了二次函数的性质,三角形的面积,主要利用了联立两函数解析式求交点坐标,难点在于三角形的面积分成两个部分求解.

练习册系列答案
相关题目
计算
-
的结果是( )
| 2 |
| a-2 |
| a |
| a-2 |
| A、1 | B、-1 | C、2 | D、-2 |
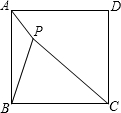 如图,P是正方形ABCD内一点,PA=3,PB=6,PC=9.求∠APB的度数.
如图,P是正方形ABCD内一点,PA=3,PB=6,PC=9.求∠APB的度数. 如图,在△ABC中,∠B=2∠C,D是三角形内一点,AB=AD,BD=DC,求证:∠ACD=30°.
如图,在△ABC中,∠B=2∠C,D是三角形内一点,AB=AD,BD=DC,求证:∠ACD=30°.