题目内容
14.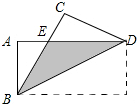 如图,把长方形ABCD沿对角线BD折叠,重合部分为△EBD.
如图,把长方形ABCD沿对角线BD折叠,重合部分为△EBD.(1)求证:△EBD为等腰三角形.
(2)图中有哪些全等三角形?
(3)若AB=6,BC=8,求△DC′E的周长.
分析 (1)根据矩形的性质得到∠BAE=∠DCE,AB=CD,再由对顶角相等可得∠AEB=∠CED,推出△AEB≌△CED,根据等腰三角形的性质即可得到结论;
(2)根据全等三角形的判定解答即可;
(3)根据三角形周长即可得到结论.
解答 解:(1)∵四边形ABCD为矩形,
∴∠BAE=∠DCE,AB=CD,
在△AEB和△CED中,
$\left\{\begin{array}{l}{∠BAE=∠DCE}\\{∠AEB=∠CED}\\{AB=CD}\end{array}\right.$,
∴△AEB≌△CED(AAS),
∴BE=DE,
∴△EBD为等腰三角形.
(2)全等三角形有:△EAB≌△EC'D;△ABD≌△CDB;△CDB≌△C'DB;△ABD≌△C'DB;
(3)△DC′E的周长=C'D+C'E+ED=AB+AE+ED=AB+AD=6+8=14.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.若x+$\frac{1}{x}$=2,则$\frac{x^2}{{{x^4}+2{x^2}+1}}$的值是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
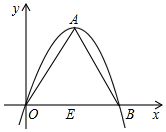 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.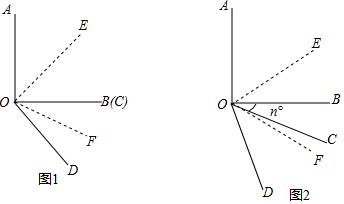
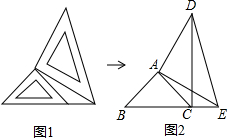 如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).
如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).