题目内容
19.已知∠AOB=90°,∠COD=30°,OE平分∠AOC,OF平分∠BOD.(1)如图1,当OB、OC重合时,求∠EOF的度数.
(2)当∠COD从图1所示位置绕点O顺时针旋转n°(0<<90)时,如图2,∠AOE-∠BOF的值是否为定值?若是定值,求出∠AOE-∠BOF的值,若不是,请说明理由.
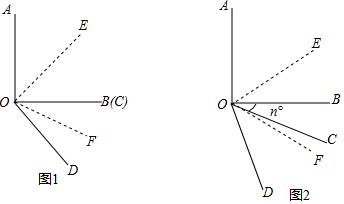
分析 (1)根据角平分线的定义知∠EOB=$\frac{1}{2}$∠AOB、∠BOF=$\frac{1}{2}$∠COD,再根据∠EOF=∠EOB+∠BOF可得答案;
(2)由题意知∠AOC=∠AOB+∠BOC=90°+n°、∠BOD=∠BOC+∠COD=n°+30°,根据角平分线的定义得$∠AOE=\frac{1}{2}$∠AOC=$\frac{90°+n°}{2}$、∠BOF=$\frac{1}{2}$∠BOD=$\frac{n°+30°}{2}$,代入计算可得.
解答 解:(1)∵OE平分∠AOC,
∴∠EOB=$\frac{1}{2}$∠AOB,
∵OF平分∠BOD,
∴∠BOF=$\frac{1}{2}$∠COD,
∴∠EOF=∠EOB+∠BOF
=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠COD
=$\frac{1}{2}$×90°+$\frac{1}{2}$×30°
=60°;
(2)是定值,
∵∠AOC=∠AOB+∠BOC=90°+n°,
∠BOD=∠BOC+∠COD=n°+30°,
∴$∠AOE=\frac{1}{2}$∠AOC=$\frac{90°+n°}{2}$,
∠BOF=$\frac{1}{2}$∠BOD=$\frac{n°+30°}{2}$,
∴∠AOE-∠BOF=$\frac{90°+n°}{2}$-$\frac{n°+30°}{2}$=30°,
∴∠AOE-∠BOF是定值.
点评 本题主要考查角的计算和角平分线的定义,熟练掌握角平分线的性质是解题的关键.

练习册系列答案
相关题目
10.甲、乙两人参加某商场的招聘测试,测试由语言和商品知识两个项目组成,他们各自的成绩(百分制)如下表所示.该商场根据成绩在两人之间录用了乙,则本次招聘测试中权重较大的是语言项目.
| 应聘者 | 语言 | 商品知识 |
| 甲 | 70 | 80 |
| 乙 | 80 | 70 |
8.9的算术平方根为( )
| A. | 9 | B. | ±9 | C. | 3 | D. | ±3 |
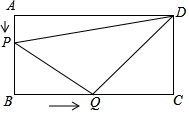 如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6). 如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为60πcm2.
如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为60πcm2.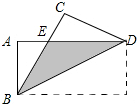 如图,把长方形ABCD沿对角线BD折叠,重合部分为△EBD.
如图,把长方形ABCD沿对角线BD折叠,重合部分为△EBD. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.∠1=∠2,∠3=105°,求∠ACB的度数.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.∠1=∠2,∠3=105°,求∠ACB的度数. 如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.
如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE. 已知图中的每个小正方格都是边长为1的小正方形,若△ABC与△A1B1C1是位似图形,且顶点都在小正方形顶点上,则它们的位似中心的坐标是(9,0).
已知图中的每个小正方格都是边长为1的小正方形,若△ABC与△A1B1C1是位似图形,且顶点都在小正方形顶点上,则它们的位似中心的坐标是(9,0).